题目内容
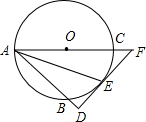 如图,过圆O外一点D作圆O的割线DBA,DE与圆O切于点E,交AO的延长线于F,AF交圆O于C,且AD⊥DE.
如图,过圆O外一点D作圆O的割线DBA,DE与圆O切于点E,交AO的延长线于F,AF交圆O于C,且AD⊥DE.(1)求证:E为
 |
| BC |
(2)若CF=3,DE•EF=
| 15 |
| 4 |
分析:要证E为
中点,可证∠EAD=∠OEA,利用辅助线OE可以证明,求EF的长需要借助相似,得出比例式,之间的关系可以求出.
 |
| BC |
解答: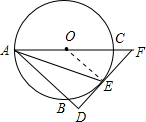 (1)证明:连接OE
(1)证明:连接OE
OA=OE=>∠OAE=∠OEA
OE切圆O于E=>OE⊥DE
AD⊥DE=>∠EAD+∠AED=90°
=>∠EAD=∠OEA
=>E为
的中点.
(2)解:连CE,则∠AEC=90°,设圆O的半径为x
∠ACE=∠AED=>Rt△ADE∽Rt△AEC=>
DE切圆O于E=>△FCE∽△FEA
∴
=
,
=
∴
=
即DE•EF=AD•CF
DE•EF=
,CF=3
∴AD=
OE∥AD=>
=
=>
=
=>8x2+7x-15=0
∴x1=1,x2=-
(舍去)
∴EF2=FC•FA=3x(3+2)=15
∴EF=
 (1)证明:连接OE
(1)证明:连接OEOA=OE=>∠OAE=∠OEA
OE切圆O于E=>OE⊥DE
AD⊥DE=>∠EAD+∠AED=90°
=>∠EAD=∠OEA
=>E为
 |
| BC |
(2)解:连CE,则∠AEC=90°,设圆O的半径为x
∠ACE=∠AED=>Rt△ADE∽Rt△AEC=>
DE切圆O于E=>△FCE∽△FEA
∴
| DE |
| AD |
| CE |
| AE |
| CE |
| AE |
| CF |
| EF |
∴
| DE |
| AD |
| CF |
| EF |
即DE•EF=AD•CF
DE•EF=
| 15 |
| 4 |
∴AD=
| 5 |
| 4 |
OE∥AD=>
| OE |
| AD |
| OF |
| AF |
| x | ||
|
| x+3 |
| 2x+3 |
∴x1=1,x2=-
| 15 |
| 8 |
∴EF2=FC•FA=3x(3+2)=15
∴EF=
| 15 |
点评:此题主要考查了圆中三角形的相似,以及证明弧相等的方法,综合性较强,通过认真的思考,一定能提升同学们的综合能力.

练习册系列答案
相关题目
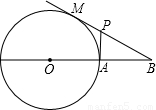
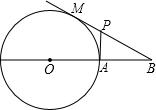 已知:如图,过圆O外一点B作圆O的切线BM,M为切点,BO交圆O于点A,过点A作BO的垂线,交BM于点P,BO=3,圆O的半径为1.求MP的长.
已知:如图,过圆O外一点B作圆O的切线BM,M为切点,BO交圆O于点A,过点A作BO的垂线,交BM于点P,BO=3,圆O的半径为1.求MP的长.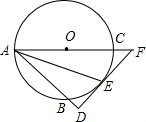 如图,过圆O外一点D作圆O的割线DBA,DE与圆O切于点E,交AO的延长线于F,AF交圆O于C,且AD⊥DE.
如图,过圆O外一点D作圆O的割线DBA,DE与圆O切于点E,交AO的延长线于F,AF交圆O于C,且AD⊥DE. 的中点;
的中点; ,求EF的长.
,求EF的长.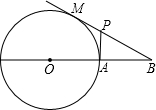 已知:如图,过圆O外一点B作圆O的切线BM,M为切点,BO交圆O于点A,过点A作BO的垂线,交BM于点P,BO=3,圆O的半径为1.求MP的长.
已知:如图,过圆O外一点B作圆O的切线BM,M为切点,BO交圆O于点A,过点A作BO的垂线,交BM于点P,BO=3,圆O的半径为1.求MP的长.