题目内容
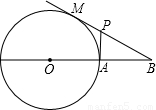
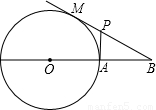
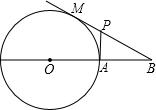 已知:如图,过圆O外一点B作圆O的切线BM,M为切点,BO交圆O于点A,过点A作BO的垂线,交BM于点P,BO=3,圆O的半径为1.求MP的长.
已知:如图,过圆O外一点B作圆O的切线BM,M为切点,BO交圆O于点A,过点A作BO的垂线,交BM于点P,BO=3,圆O的半径为1.求MP的长.
分析:连接OM,根据切线的性质得到直角三角形,根据勾股定理求得BM的长.再根据切线长定理和勾股定理列方程求得MP的长.
解答: 解:连接OM,则OM⊥BM,
解:连接OM,则OM⊥BM,
在Rt△BOM中,OM=1,BO=3,
根据勾股定理,得BM=2
;
∵AP⊥OB,
∴AP是圆的切线,
又PM是圆的切线,
∴AP=MP;
在Rt△APB中,
设AP=x,AB=3-1=2,BP=2
-x;
根据勾股定理得:
(2
-x)2=x2+4
x=
.
 解:连接OM,则OM⊥BM,
解:连接OM,则OM⊥BM,在Rt△BOM中,OM=1,BO=3,
根据勾股定理,得BM=2
| 2 |
∵AP⊥OB,
∴AP是圆的切线,
又PM是圆的切线,
∴AP=MP;
在Rt△APB中,
设AP=x,AB=3-1=2,BP=2
| 2 |
根据勾股定理得:
(2
| 2 |
x=
| ||
| 2 |
点评:此题综合运用了勾股定理和切线的判定以及切线长的定理.

练习册系列答案
相关题目
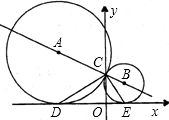 已知:如图,OA与oB外切于点C,DE是两圆的一条外公切线,切点分别为D、E.
已知:如图,OA与oB外切于点C,DE是两圆的一条外公切线,切点分别为D、E.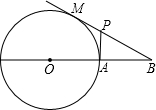 已知:如图,过圆O外一点B作圆O的切线BM,M为切点,BO交圆O于点A,过点A作BO的垂线,交BM于点P,BO=3,圆O的半径为1.求MP的长.
已知:如图,过圆O外一点B作圆O的切线BM,M为切点,BO交圆O于点A,过点A作BO的垂线,交BM于点P,BO=3,圆O的半径为1.求MP的长.