题目内容
等腰三角形底边长10厘米,腰长13厘米,则底边上的高等于
- A.6 厘米
- B.8 厘米
- C.12 厘米
- D.8或12厘米
C
分析:在等腰三角形的腰和底边高线所构成的直角三角形中,根据勾股定理即可求得底边上高线的长度.
解答:如图:AB=AC=13cm,BC=10cm.
∵△ABC中,AB=AC,AD⊥BC;
∴BD=DC= BC=5cm;
BC=5cm;
∵在Rt△ABD中,AB=13cm,BD=5cm;
∴AD=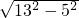 =12(cm).
=12(cm).
故选:C.
点评:本题主要考查了等腰三角形的性质以及勾股定理的应用.关键是掌握等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
分析:在等腰三角形的腰和底边高线所构成的直角三角形中,根据勾股定理即可求得底边上高线的长度.
解答:如图:AB=AC=13cm,BC=10cm.

∵△ABC中,AB=AC,AD⊥BC;
∴BD=DC=
 BC=5cm;
BC=5cm;∵在Rt△ABD中,AB=13cm,BD=5cm;
∴AD=
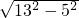 =12(cm).
=12(cm).故选:C.
点评:本题主要考查了等腰三角形的性质以及勾股定理的应用.关键是掌握等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目