题目内容
3.解方程组:$\left\{\begin{array}{l}{\frac{2}{x-y}+\frac{1}{x+y}=\frac{1}{4}}\\{\frac{1}{x+y}-\frac{1}{x-y}=1}\end{array}\right.$.分析 设$\frac{1}{x-y}$=a,$\frac{1}{x+y}$=b,方程组变形后求出解得到a与b的值,即可确定出x与y的值.
解答 解:设$\frac{1}{x-y}$=a,$\frac{1}{x+y}$=b,
方程组变形得:$\left\{\begin{array}{l}{2a+b=\frac{1}{4}①}\\{b-a=1②}\end{array}\right.$,
①-②得:3a=-$\frac{3}{4}$,即a=-$\frac{1}{4}$,
把a=-$\frac{1}{4}$代入②得:b=$\frac{3}{4}$,
可得$\left\{\begin{array}{l}{x-y=-4}\\{x+y=\frac{4}{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-\frac{4}{3}}\\{y=\frac{8}{3}}\end{array}\right.$,
则经检验$\left\{\begin{array}{l}{x=-\frac{4}{3}}\\{y=\frac{8}{3}}\end{array}\right.$是方程组的解.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
13.小明做了如下四个因式分解题,你认为小明做得对得不完整一题是( )
| A. | x2y-xy2=xy(x-y) | B. | m2-2mn+n2=(m-n)2 | C. | a3-a=a(a2-1) | D. | -x2+y2=(y+x)(y-x) |
18.已知三角形三边长分别为5cm、5cm、6cm,则这个三角形内切圆的半径是( )
| A. | $\frac{9}{8}$cm | B. | $\frac{3}{2}$cm | C. | 2cm | D. | 3cm |
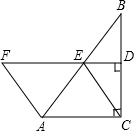 已知,Rt△ABC,∠ACB=90°,BC的垂直平分线DE交BC于D,AF=CE.求证:四边形ACEF是平行四边形.
已知,Rt△ABC,∠ACB=90°,BC的垂直平分线DE交BC于D,AF=CE.求证:四边形ACEF是平行四边形. 如图,已知?ABCD中,AE⊥BC,点E是垂足,AE与BD交于点G,且DG=2AB,∠DBC=25°.求∠ABD的度数.
如图,已知?ABCD中,AE⊥BC,点E是垂足,AE与BD交于点G,且DG=2AB,∠DBC=25°.求∠ABD的度数.