Question

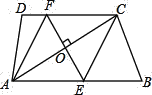
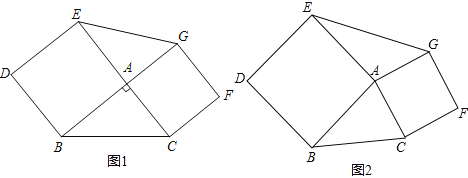
【题目】以△ABC的边AB，AC为边分别向外作正方形ABDE和正方形ACFG，连接EG，M为EG的中点，连接AM．

（1）如图1，∠BAC=90°，试判断AM与BC关系？

（2）如图2，∠BAC≠90°，图1中的结论是否成立？若不成立，说明理由；若成立，给出证明．

Answer 1

【答案】(1)证明见解析；(2)结论仍然成立，理由见解析.

【解析】

（1）结论：AM=BC．易知AM=EG，只要证明△BAC≌△EAG即可解决问题；

（2）结论仍然成立．延长AM到N，使得AM=MN，连接EN、NG．只要证明△BAC≌△AEN，即可解决问题．

（1）结论：AM=BC．

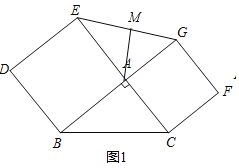
理由：∵∠BAC=∠EAG=90°，EM=GM，

∴AM=EG，

在△BAC和△EAG中，

，

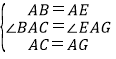∴△BAC≌△EAG，

∴BC=EG，

∴AM=BC．

(2)（1）中结论仍然成立．

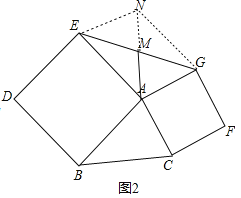
理由：延长AM到N，使得AM=MN，连接EN、NG．

∴EM=MG，AM=MN，

∴四边形AENG是平行四边形，

∴EN=AG，EN∥AG，

∴∠NEA+∠EAG=180°，

∵∠BAE=∠CAG=90°，

∴∠BAC+∠EAG=180°，

∴∠NEA=∠BAC，

∵AB=AE，AC=EN，

∴△BAC≌△AEN，

∴BC=AN，

∴AM=BC．