题目内容
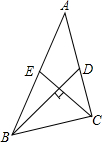△ABC中，BD和CE分别是AC和AB上的中线，且BD与CE互相垂直，BD=8，CE=12，则△ABC的面积是64
64
．分析：先画出图形，连接DE，过点E作EF∥BD，交CB的延长线于点F．由BD⊥CE，BD=8，CE=12，得CF=10，根据中位线的性质，求得DE，即得出BF=
CF，S△BEC=S△ACE=S△CEF，从而得出△ABC的面积．
| 1 |
| 3 |
解答：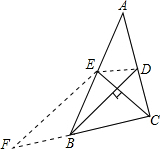
解：连接DE，过点E作EF∥BD，交CB的延长线于点F．
∵BD和CE分别是两边上的中线，
∴DE=
BC，
∵四边形BDEF为平行四边形，
∴BF=DE，
∴BF=
CF，
∴S△BEF=
S△CEF，
∵S△BEC=S△ACE，
∴S△ABC=
S△CEF=
×12×8÷2=64．
故答案为：64．
解：连接DE，过点E作EF∥BD，交CB的延长线于点F．∵BD和CE分别是两边上的中线，
∴DE=
| 1 |
| 2 |
∵四边形BDEF为平行四边形，
∴BF=DE，
∴BF=
| 1 |
| 3 |
∴S△BEF=
| 1 |
| 3 |
∵S△BEC=S△ACE，
∴S△ABC=
| 4 |
| 3 |
| 4 |
| 3 |
故答案为：64．
点评：本题考查了三角形的中位线定理和三角形面积的求法，此类题型需要同学们熟练掌握．
练习册系列答案
相关题目
15、如图，在△ABC中，BD和CD分别是∠ABC和∠ACB的平分线，EF过D点．且EF∥BC，若BE=5，CF=3，则EF=
（2013•遵义模拟）如图，△ABC中，BD和CE是两条高，如果∠A=45°，则
如图，锐角△ABC中，BD和CE分别是AC和AB的高，若BD和CE所夹的锐角为61°，则∠ABC+∠ACB=
如图，在△ABC中，BD和CE分别平分∠ABC和∠ACB．