题目内容
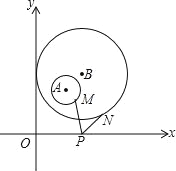
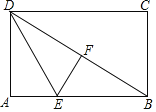
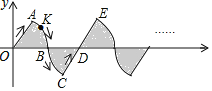
【题目】在平面直角坐标系xOy中，若干个半径为1个单位长度，圆心角是
的扇形按图中的方式摆放，动点K从原点O出发，沿着“半径OA
弧AB弧BC半径CD半径DE
”的曲线运动，若点K在线段上运动的速度为每秒1个单位长度，在弧线上运动的速度为每秒
个单位长度，设第n秒运动到点K，
为自然数
，则
的坐标是____，
的坐标是____
【答案】
【解析】
设第n秒运动到Kn（n为自然数）点，根据点K的运动规律找出部分Kn点的坐标，根据坐标的变化找出变化规律“K4n+1（
），K4n+2（2n+1，0），K4n+3（
），K4n+4（2n+2，0）”，依此规律即可得出结论．
设第n秒运动到Kn（n为自然数）点，观察，发现规律：K1（
），K2（1，0），K3（
），K4（2，0），K5（
），…，∴K4n+1（），K4n+2（2n+1，0），K4n+3（），K4n+4（2n+2，0）．
∵2018=4×504+2，∴K2018为（1009，0）．
故答案为：（），（1009，0）．
A加金题 系列答案
全优测试卷系列答案
【题目】某食品厂生产一种半成品食材，产量
百千克
与销售价格
元
千克满足函数关系式
，从市场反馈的信息发现，该半成品食材的市场需求量
百千克与销售价格元千克满足一次函数关系，如下表：
销售价格 | 2 | 4 |
| 10 |
市场需求量 | 12 | 10 |
| 4 |
已知按物价部门规定销售价格x不低于2元千克且不高于10元千克
求q与x的函数关系式；
当产量小于或等于市场需求量时，这种半成品食材能全部售出，求此时x的取值范围；
当产量大于市场需求量时，只能售出符合市场需求量的半成品食材，剩余的食材由于保质期短而只能废弃
若该半成品食材的成本是2元千克．
求厂家获得的利润
百元与销售价格x的函数关系式；
当厂家获得的利润百元随销售价格x的上涨而增加时，直接写出x的取值范围
利润
售价
成本
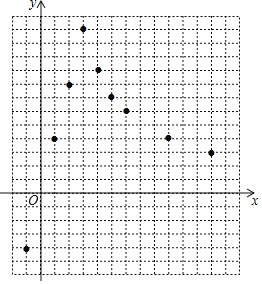
【题目】初三某班同学小戴想根据学习函数的经验，通过研究一个未学过的函数的图象，从而探究其各方面性质．
下表是函数y与自变量x的几组对应值：
x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 9 | 12 | … |
y | … | -4 | 0 | 4 | 8 | 12 | 9 | 7.2 | 6 | 4 | 3 | … |
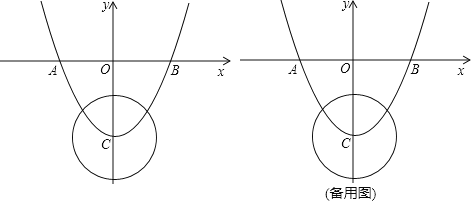
（1）在平面直角坐标系xOy中，每个小正方形的边长为一个单位长度，描出了以上表中各对对应值为坐标的点，请根据描出的点，画出该函数的图象．
（2）请根据画出的函数图象，直接写出该函数的关系式y=______（请写出自变量的取值范围），并写出该函数的一条性质：______．
（3）当直线y=-
x+b与该函数图象有3个交点时，求b的取值范围．
