题目内容
如图,已知Rt△ABC,∠ABC=90º,以直角边AB为直径作⊙O,交斜边AC于点D,连结BD.
(1)若AD=3,BD=4,求边BC的长;
(2)取BC的中点E,连结ED,试证明ED与⊙O相切.
(1) (2)通过连接OD,证明
(2)通过连接OD,证明 ,则可得到ED与⊙O相切.
,则可得到ED与⊙O相切.
解析试题分析:(1)∵AB是直径,∴ ,∵
,∵ ,
, ,∴
,∴ ,
,
∵ ,
, ,∴△ADB∽△ABC,
,∴△ADB∽△ABC,
∴ ,∴
,∴ ,
,
(2)要证明圆与直线相切,即证明圆与其切点所对应的的直径成直角,根据题意,可以证得其为直角
证明:连结OD,在Rt△BDC中,∵E是BC的中点,∴ ,
,
∴ ,又
,又 ,∴
,∴ ,又∵
,又∵ ,
, ,
,
∴ ,∵AB是直径,∴
,∵AB是直径,∴ ,∴
,∴ ,∴
,∴ ,
, ,∴
,∴ ,∴
,∴ ,∴ED与⊙O相切.
,∴ED与⊙O相切.
考点:相似三角形的判断及其性质,圆与直线相切的证明
点评:相似三角形,对应边成比例,圆与直线相切,即证明圆与其切点所对应的的直径成直角

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.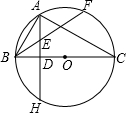 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF. 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P. 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为