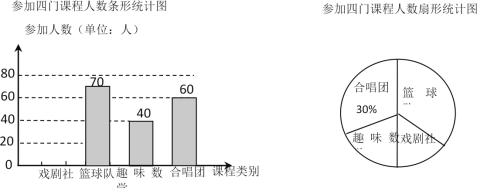
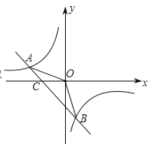
��Ŀ����
����Ŀ����֪����ͼ,��Rt��ABO��,��B=90��,��OAB=30��,OA=3.�Ե�OΪԭ��,б��OA����ֱ��Ϊx��,����ƽ��ֱ������ϵ,�Ե�P(4,0)ΪԲ��,PA��Ϊ�뾶��Բ,��P��x�����һ����ΪN,��M�ڡ�P��,�������MPN=60��.��P��ÿ��1����λ���ȵ��ٶ���x�������˶������˶�ʱ��Ϊts������������⣺
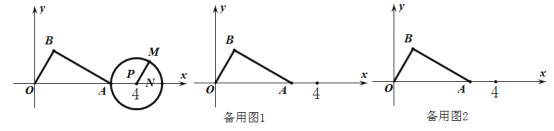
(1)�˶������е���A�ڡ�P��ʱ��t��ȡֵ��Χ�� ��
(2)����P����ABO�ı�����ʱ�����P�����ꣻ
(3)����MN��Rt��ABO�ı�����������ʱ������ֱ��д��t��ȡֵ��Χ.
���𰸡���1��0<t<2����2����1,0����![]() ��0������3��2��t��3��4��t��5.
��0������3��2��t��3��4��t��5.
��������
��1���������⣬��2<OP<4ʱ����A�ڡ�P�ڣ��Ӷ���t��ȡֵ��Χ��
��2����Բ��ֱ��AB��ֱ��OB���У��������Ǻ������ɵó����ۣ�
��3�����ҳ�![]() ��ֱ�������ε���������������ʱ�ķֽ�㣬���ɵó����ۣ�
��ֱ�������ε���������������ʱ�ķֽ�㣬���ɵó����ۣ�
�⣺��1����OA=3��P(4,0)
��OP=4��AP=1
�֡ߡ�P��ÿ��1����λ���ȵ��ٶ���x�������˶�
�൱2<OP<4ʱ����A�ڡ�P�ڣ����˶�ʱ��Ϊts��
��OP=4-t
��2<4-t<4
��ã�0<t<2��
��2������ͼ2������P��ֱ��AB�����ڵ�Cʱ

����PC������PC��AB��PC=r=1��
�ߡ�OAB=30����
��AP=2��
��OP=OA-AP=3-2=1��
���P��������1��0����
����ͼ3������P��ֱ��OB�����ڵ�Dʱ��

����PD������PD��OB��PD=r=1��
��PD��AB��
���OPD=��OAB=30����
��cos��OPD=![]() ��
��
��OP=![]() ��
��
���P������Ϊ![]()
����������P��������1��0����![]() ��
��
��3�� t��ȡֵ��Χ��2��t��3��4��t��5��
���ɣ���ͼ5������N�˶������A�غ�ʱ��

![]() ��Rt��ABO�ı���һ�������㣬
��Rt��ABO�ı���һ�������㣬
��ʱt=2��
��t��2��ֱ����P�˶�����AB����ʱ��
��̽���ٵã�OP=1��
��![]() ��
��
![]() ��Rt��ABO�ı������������㣬
��Rt��ABO�ı������������㣬
��2��t��3��
��ͼ6������P�˶���PM��OB�غ�ʱ��

![]() ��Rt��ABO�ı������������㣬
��Rt��ABO�ı������������㣬
��ʱt=4��
ֱ����P�˶�����N���O�غ�ʱ��
![]() ��Rt��ABO�ı���һ�������㣬
��Rt��ABO�ı���һ�������㣬
��ʱt=5��
��4��t��5��
����t��ȡֵ��Χ��2��t��3��4��t��5��

 ��У����ϵ�д�
��У����ϵ�д�