��Ŀ����
����Ŀ���ҹ��Ŵ���ѧ������������������������һ�����⣺���гط�һ�ɣ����������룬��ˮһ�ߣ����縰�������ڰ��룬��ˮ��糤�����Σ�����������˼��˵������һ���߳�Ϊ10�ߵ�������ˮ�أ���ˮ�ص������볤��һ��«έ��«έ¶��ˮ��1�ߣ�����«έ����ˮ��һ�ߵ��е㴦��«έ�Ķ���ǡ�õ���رߵ�ˮ�棬��ˮ����������«έ�ij��ȷֱ��Ƕ��٣�����ˮ�����Ϊx�ߣ�����Եõ�����_____��
���𰸡�x2+52����x+1��2��
��������
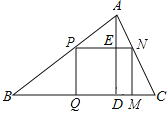
���ǿ��Խ���ת��Ϊ��ѧ����ͼ�Σ���ͼ��ʾ���������⣬��֪EB'�ij�Ϊ10�ߣ���B'C��5�ߣ����AB��AB'��x�ߣ���ʾ��ˮ��AC�����ݹ��ɶ����������̼��ɣ�
�����⻭��ͼ�Σ�
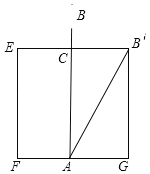
��«έ��AB��AB����x�ߣ���ˮ��AC����x��1���ߣ���ΪB'E��10�ߣ�����B'C��5�ߣ�
��Rt��AB'C����CB��2+AC2��AB��2
��52+��x��1��2��x2��
�ʴ�Ϊ��x2+52����x+1��2��

��ϰ��ϵ�д�
 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�
�����Ŀ