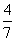题目内容
如图,△ABC为等腰三角形,AB=AC,O是底边BC的中点,⊙O与腰AB相切于点D,求证:AC与⊙O相切.

考点: 切线的判定;等腰三角形的性质.
专题: 证明题.
分析: 欲证AC与⊙O相切,只要证明圆心O到AC的距离等于圆的半径即可,即连接OD,过点O作OE⊥AC于E点,证明OE=OD.
解答: 证明:连接OD,过点O作OE⊥AC于E点,
则∠OEC=90°,
∵AB切⊙O于D,
∴OD⊥AB,
∴∠ODB=90°,
∴∠ODB=∠OEC;(3分)
又∵O是BC的中点,
∴OB=OC,
∵AB=AC,
∴∠B=∠C,
∴△OBD≌△OCE,(6分)
∴OE=OD,即OE是⊙O的半径,
∴AC与⊙O相切.(9分)

点评: 本题考查了学生对切线的判定的理解及运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
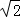 cm C. 5πcm D. 5
cm C. 5πcm D. 5 交于A(x1,y1),B(x2,y2)两点,则2x1y2﹣7x2y1= .
交于A(x1,y1),B(x2,y2)两点,则2x1y2﹣7x2y1= .
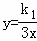 的图象与一次函数y=k2x+m的图象交于A(﹣1,a)、B(
的图象与一次函数y=k2x+m的图象交于A(﹣1,a)、B(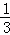 ,﹣3)两点,连结AO.
,﹣3)两点,连结AO.

 )÷(﹣1
)÷(﹣1 )+(﹣2)2×(﹣3)
)+(﹣2)2×(﹣3)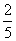 B.
B.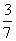 C.
C.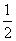 D.
D.