Question

如图，已知Rt△ABC中，∠A=30°，AC=6．边长为4的等边△DEF沿射线AC运动（A、D、E、C四点共线）．

（1）当等边△DEF的边DF、EF与Rt△ABC的边AB分别相交于点M、N（M、N不与A、B重合）时．
①试判定△FMN的形状，并说明理由；
②若以点M为圆心，MN为半径的圆与边AC、EF同时相切，求此时MN的长．
（2）设AD=x，△ABC与△DEF重叠部分的面积为y，求y关于x的函数解析式，并写出x的取值范围．

Answer 1

解：（1）如图1，①∵△DEF是等边三角形，
∴∠FDE=∠F=60°．
∵∠A=30°，
∴∠AMD=∠FDE-∠A=30°，
∴∠FMN=∠AMD=30°，
∴∠MNF=90°，
即△FMN是直角三角形，
②如图2，过点M作MG⊥AC于点G，
设DM=x，
∵∠MDG=60°，
∴MG=，
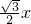又∵△FMN是直角三角形，∠MFN=60°，
∴MN==，
∵以点M为圆心，MN为半径的圆与边AC、EF同时相切，
则有MG=MN，
即，
解得：x=2．
∴圆的半径MN=；

（2）∵∠AMD=∠A=30°，
∴DM=AD，
∴DM=AD=x，FM=4-x．
又∵△FMN是直角三角形，∠MFN=60°
∴MN=MF•sinF=（4-x）×=（4-x），
FN=MF=（4-x），
S_△FMN=MN•FN=×（4-x）×（4-x）=（4-x）²．
①当0＜x≤2时，S_{四边形DENM}=S_△FDE-S_△FMN=4-（4-x）²=-x²+x+2，
②当2＜x＜4时，
CE=AE-AC=4+x-6=x-2．
∵∠BCE=90°，∠PEA=60°，
∴PC=，
∴S_△PCE=×（x-2）（x-2）=（x-2）²．
∴y_{五边形DCPNM}=S_△DEF-S_△FMN-S_△PCE=，
③如图3，当4≤x＜6时，CD=6-x，
∵∠BCE=90°，∠PDC=60°，
∴PC=，
∴y=S_△PCD=×（6-x）（6-x）=（6-x）²，
④当x≥6时 y=0．
分析：（1）①根据已知得出∠AMD=∠FDE-∠A=30°，进而得出∠MNF=90°，
②设DM=x，根据∠MDG=60°，得出MG=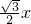，进而得出MN=，利用MG=MN，求出即可；
（2）分别根据当0＜x≤2时，S_{四边形DENM}=S_△FDE-S_△FMN，②当2＜x＜4时，y_{五边形DCPNM}=S_△DEF-S_△FMN-S_△PCE，
③如图3，当4≤x＜6时，CD=6-x，y=S_△PCD，④当x≥6时，y=0，得出即可．
点评：本题考查了圆的综合题，涉及到直角三角形的性质、锐角三角函数的定义、三角形的面积等知识，难度适中，注意自变量x的取值范围的分析与讨论．