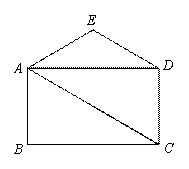
题目内容
如图,点F在□ABCD的对角线AC上,过点F、 B分别作AB、
AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
(1)求证:四边形ABEF是菱形;
(2)若BE=5,AD=8,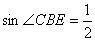 ,求AC的长.
,求AC的长.

(1)证明:∵EF∥AB,BE∥AF,
∴四边形ABEF是平行四边形.
∵∠ABF=∠ FBC+∠FCB,∠AFB=∠FBC+∠FCB,
FBC+∠FCB,∠AFB=∠FBC+∠FCB,
∴∠ABF=∠AFB. …………………………………………………………………1分
∴AB=AF.
∴□ABEF是菱形. ………………………………………………………………2分
(2)解:作DH⊥AC于点H,
 ∵
∵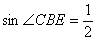 ,
,
∴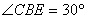 .
.
∵BE∥AC,
∴ .
.
∵AD∥BC,
∴ .
.
∴ .
.
Rt△ADH中,
 .………………………………………………3分
.………………………………………………3分
 .
.
∵四边形ABEF是菱形,
∴CD= AB=BE=5,
Rt△CDH中,
 . ………………………………………………4分
. ………………………………………………4分
∴ .……………………………………
.…………………………………… ……5分
……5分

练习册系列答案
相关题目
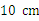 ,宽为
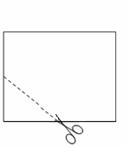
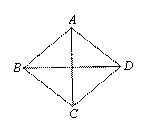
,宽为 的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )
的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( ) B.
B. C.
C.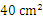 D.
D.
 ,记下数字为y. 计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率.
,记下数字为y. 计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率. 的值为0,则x的值为 .
的值为0,则x的值为 . .
. ,PB= .
,PB= . (2)对于点P的其他位置,是否始终具有②中的结论?若是,请证明;若不是,请举例说明.
(2)对于点P的其他位置,是否始终具有②中的结论?若是,请证明;若不是,请举例说明.
 米,则扇形OAB的面积为
米,则扇形OAB的面积为 平方米 B.
平方米 B.  平方米
平方米  平方米 D.
平方米 D.  平方米
平方米
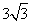 ,求平行线DE与AC间的距离.
,求平行线DE与AC间的距离.