题目内容
1.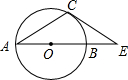 如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠A=30°,则sin∠E的值为( )
如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠A=30°,则sin∠E的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 首先连接OC,由CE是⊙O切线,可证得OC⊥CE,又由圆周角定理,求得∠BOC的度数,继而求得∠E的度数,然后由特殊角的三角函数值,求得答案.
解答 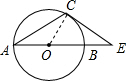 解:连接OC,
解:连接OC,
∵CE是⊙O切线,
∴OC⊥CE,
∵∠A=30°,
∴∠BOC=2∠A=60°,
∴∠E=90°-∠BOC=30°,
∴sin∠E=sin30°=$\frac{1}{2}$.
故选A.
点评 此题考查了切线的性质、圆周角定理以及特殊角的三角函数值.注意准确作出辅助线是解此题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
13.菱形ABCD中,对角线AC、BD相交于O,H为AD边中点,OH的长等于3,则菱形ABCD的周长为( )
| A. | 24 | B. | 12 | C. | 9 | D. | 18 |
9.下列各数中最小的是( )
| A. | 0 | B. | -3 | C. | -$\sqrt{3}$ | D. | 1 |
12.不等式组:$\left\{\begin{array}{l}{3x-1<x+1}\\{2(2x-1)≤5x+1}\end{array}\right.$的最大整数解为( )
| A. | 1 | B. | -3 | C. | 0 | D. | -1 |
8.2016年“五一”假期期间,某市接待旅游总人数达到了9 180 000人次,将9 180 000用科学记数法表示应为( )
| A. | 918×104 | B. | 9.18×105 | C. | 9.18×106 | D. | 9.18×107 |
 如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( )
如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( ) 如图,在?ABCD中,已知AD>AB.
如图,在?ABCD中,已知AD>AB. 如图,已知BD是矩形ABCD的对角线.
如图,已知BD是矩形ABCD的对角线.