Question

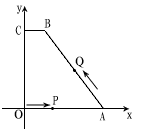
已知如图所示，在平面直角坐标系中，四边形ABC0为梯形，BC∥AO，四个顶点坐标分别为A（4，0），B（1，4），C（0，4），O（0，0）。一动点P从O出发以每秒1个单位长度的速度沿OA的方向向A运动；同时，动点Q从A出发，以每秒2个单位长度的速度沿A→B→C的方向向C运动。两个动点若其中一个到达终点，另一个也随之停止．设其运动时间为t秒。
（1）求过A，B，C三点的抛物线的解析式；
（2）当t为何值时，PB与AQ互相平分；
（3）连接PQ，设△PAQ的面积为S，探索S与t的函数关系式，求t为何值时，S有最大值？最大值是多少？

Answer 1

解：（1）设抛物线的解析式为，代入A、B、C三点，得
 
∴
∴；
（2）使得PB与AQ互相平分，故，
∴，
∴，，
，；
（3）由已知得AB=5，CB=1，
①当时，点Q在线段AB上运动，
设，∠OAB=θ，sinθ=，
∴，
∵，
∴，
∴当时，有最大值为；
②当时，点Q在线段BC上运动，则，
∴当时，有最大值为3，
∴综上所述，当时，有最大值为。