题目内容
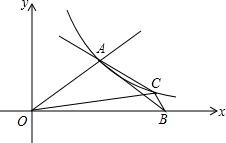 如图,直线y=
如图,直线y=
| ||
| 3 |
| ||
| x |
(1)求B点的坐标;
(2)C为y=
| ||
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)联立方程即可求得交点坐标A,然后根据等腰三角形的性质即可求得B的坐标;
(2)作∠CAD=120°,交BC的延长线于点D,由直线的斜率求得∠AOB=30°,进而求得∠OAB=120°,然后求得△AOC≌△ABD,得出OC=BD=BC+CD,AC=AD,根据等腰三角形,通过解直角三角形求得CD=
AC,即可求得OC=BC+
AC.
(2)作∠CAD=120°,交BC的延长线于点D,由直线的斜率求得∠AOB=30°,进而求得∠OAB=120°,然后求得△AOC≌△ABD,得出OC=BD=BC+CD,AC=AD,根据等腰三角形,通过解直角三角形求得CD=
| 3 |
| 3 |
解答: 解:(1)∵直线y=
解:(1)∵直线y=
x与反比例函数y=
(x>0)交于A点,
∴A点的坐标(
,1),
∵OA=AB.
∴B(2
,0).
(2)OC=BC+
AC,理由如下:
作∠CAD=120°,交BC的延长线于点D,
由直线y=
x可知∠AOB=30°,
∵OA=AB,
∴∠ABO=30°,
∴∠OAB=120°,
∴∠OAC=120°+∠BAC=∠BAD,
∴∠ABC+∠ABO+∠BOC=180°-∠OCB=60°,
∴∠ABC+∠BOC=60°-∠ABO=30°,
∵∠AOC+∠BOC=30°,
∴∠AOC=∠ABC=∠ABD,
在△AOC和△ABD中
∴△AOC≌△ABD(ASA),
∴OC=BD=BC+CD,AC=AD,
∵∠CAD=120°,
∴CD=
AC,
∴OC=BC+
AC.
 解:(1)∵直线y=
解:(1)∵直线y=
| ||
| 3 |
| ||
| x |
∴A点的坐标(
| 3 |
∵OA=AB.
∴B(2
| 3 |
(2)OC=BC+
| 3 |
作∠CAD=120°,交BC的延长线于点D,
由直线y=
| ||
| 3 |
∵OA=AB,
∴∠ABO=30°,
∴∠OAB=120°,
∴∠OAC=120°+∠BAC=∠BAD,
∴∠ABC+∠ABO+∠BOC=180°-∠OCB=60°,
∴∠ABC+∠BOC=60°-∠ABO=30°,
∵∠AOC+∠BOC=30°,
∴∠AOC=∠ABC=∠ABD,
在△AOC和△ABD中
|
∴△AOC≌△ABD(ASA),
∴OC=BD=BC+CD,AC=AD,
∵∠CAD=120°,
∴CD=
| 3 |
∴OC=BC+
| 3 |
点评:本题考查了反比例函数和一次函数的交点,等腰三角形的性质以及全等三角形的判定和性质,作出辅助线构建全等三角形是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列计算结果为负值的是( )
| A、(-3)÷(-2) |
| B、0×(-7)×3 |
| C、-1-9 |
| D、-7-(-10) |
某市近五年国民消费指数增长率分别为8.5%,9.2%,9.9%,10.2%,11.2%.业内人士评论说:“这五年消费指数增长率相当平稳”,从统计角度看,“增长率相当平稳”说明下列哪个统计量比较小.( )
| A、方差 | B、平均数 |
| C、众数 | D、中位数 |
掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,则向上的一面的点数为4的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
| (-2)2 |
A、-
| ||
| B、-2 | ||
| C、2 | ||
D、
|
若|a+2|=5,则数轴上有理数a对应的点与-1对应的点的距离是( )
| A、2 | B、4 | C、2或8 | D、4或6 |
 如图是一个长方形试管架,在23cm长的木条上钻了4个圆孔,每个孔的半径为1cm,则x等于
如图是一个长方形试管架,在23cm长的木条上钻了4个圆孔,每个孔的半径为1cm,则x等于