题目内容
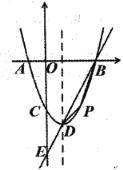
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于
轴交于![]() 点,抛物线顶点为
点,抛物线顶点为![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() 点.
点.
(1)求抛物线函数表达式;
(2)若点![]() 是位于直线
是位于直线![]() 下方抛物线上的一动点,以
下方抛物线上的一动点,以![]() 、
、![]() 为相邻的两边作平行四边形
为相邻的两边作平行四边形![]() ,当平行四边形
,当平行四边形![]() 的面积最大时,求此时平行四边形
的面积最大时,求此时平行四边形![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)平行四边形PBFD的面积S为2,P(2,-3);(3)存在.点G的坐标为
;(2)平行四边形PBFD的面积S为2,P(2,-3);(3)存在.点G的坐标为![]() .
.
【解析】
(1)先设抛物线的顶点式,然后利用待定系数法,即可求出解析式;
(2)根据题意,先求出BD的解析式,当PF的值最大时,面积取到最大值,即可得到答案;
(3)先证明![]() ,设点G的坐标为
,设点G的坐标为![]() ,利用三角函数值,求出t的值,即可得到点G的坐标.
,利用三角函数值,求出t的值,即可得到点G的坐标.
解:(1)设抛物线为![]()
把A(![]() 1,0),C(0,
1,0),C(0,![]() 3)代入得
3)代入得
![]() 得:
得:![]() ,
,
![]() ,
,
即![]() ;
;
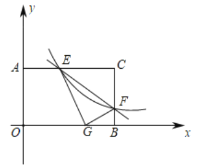
(2)设直线BD为y=kx+b,如图,过点P作PF⊥x轴交直线BD于F,

将点(1,![]() 4)、(3,0)代入y=kx+b中,
4)、(3,0)代入y=kx+b中,
解得,k=2,b=![]() 6,
6,
∴BD解析式为y=2x-6,
设点P(a,a2-2a-3),则F(a,2a-6),
则PF=2a-6-(a2-2a-3)
=-a2+4a-3
当a=2时,PF有最大长度1,
∴S△PBD最大=S△PBF+S△PDF
=![]() PF2=1
PF2=1
∴以PB、PD为相邻的两边作平行四边形PBFD,当平行四边形MANB的面积最大时,
S最大=2S△PBD最大=2×1=2,
∴P(2,-3);
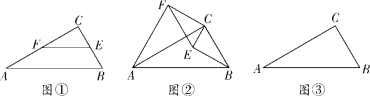
(3)存在.如图2,
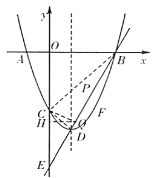
由B(3,0),C(0,-3),D(1,-4)可知,
BC=![]() ,CD=
,CD=![]() ,BD=
,BD=![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点G在线段BD上,所以设点G的坐标为![]() ,
,
过点G作GH⊥y轴于点H,当tan∠GCH=3时,∠BDC=∠GCE,
![]()
解得:![]()
∴![]() ,
,
∴点G的坐标为:![]() .
.

【题目】为进一步提升教育教学质量,调动学生学习的兴趣,某校在七年级学生中开展了对语文、数学、英语、历史、地理这五门课程的兴趣爱好情况的调查,以便采取必要教学改革,激发学生对各学科的兴趣爱好.随机选取该年级部分学生进行调查,要求每名学生从中选出一门最感兴趣的课程(每名学生只能选一门,不能多选),以下是根据调查结果绘制的不完整统计图表:
课程代号 |
|
|
|
|
|
课程名称 | 语文 | |数学 | 英语 | 历史 | 地理 |
最感兴趣人数 | 12 | 30 |
| 54 | 9 |
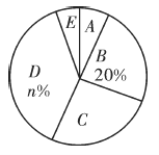
请你根据以上信息,解答下列问题:
(1)被调查学生的总数为______人,![]() ______,
______,![]() ______;
______;
(2)被调查学生中,最喜爱课程的“众数”是______;
(3)若该年级共有800名学生,请估计该年级对语文最感兴趣的学生人数.
【题目】某市少年宫为小学生开设了绘画、音乐、舞蹈和跆拳道四类兴趣班,为了解学生对这四类兴趣班的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了一幅不完整的统计表
最受欢迎兴趣班调查问卷 | 统计表 | |||||
选项 | 兴趣班 | 请选择 | 兴趣班 | 频数 | 频率 | |
A | 绘画 | A | 0.35 | |||
B | 音乐 | B | 18 | 0.30 | ||
C | 舞蹈 | C | 15 |
| ||
D | 跆拳道 | D | 6 | |||
你好!请选择一个(只能选一个)你最喜欢的兴趣班,在其后空格内打“√”,谢谢你的合作. |
| 1 | ||||
请你根据统计表中提供的信息回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)根据调查结果,请你估计该市2000名小学生中最喜欢“绘画”兴趣的人数;
(3)王姝和李要选择参加兴趣班,若他们每人从A、B、C、D四类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类的概率.