题目内容
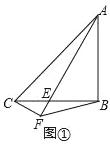
【题目】如图，在△ABC中，∠ABC=90°，AB=BC，点E是直线BC上一点，连接AE，过点C作CF⊥AE于点F，连接BF．如图①，当点E在BC上时，易证AF﹣CF=
BF（不需证明），点E在CB的延长线上，如图②：点E在BC的延长线上，如图③，线段AF，CF，BF之间又有怎样的数量关系？请直接写出你的猜想，并选择一种情况给予证明．
【答案】证明AF=CF+
BF．
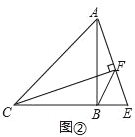
如图②中，结论：CF﹣AF=BF．理由见解析；②如图③中，结论：CF+AF=BF．理由见解析.
【解析】
如图①中，作BH⊥BF交AF于H．只要证明△BAH
△BCF，即可解决问题.
①如图②中，结论：CF－AF＝BF．作BH⊥BF交AF于H．只要证明△BAH△BCF，即可解決问題.
②如图③中，结论：CF＋AF＝BF，只要证明△BAH△BCF，即可解決问题.
证明：如图①中，作BH⊥BF交AF于H．
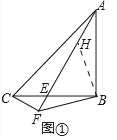
∵∠ABC=∠FBH，
∴∠FBC=∠ABH，
∵∠EFC=∠EBA=90°，
∠CEF=∠AEB，
∴∠ECF=∠EAB，
在△BAH和△BCF中，
，
∴△BAH≌△BCF，
∴AH=CF，BH=BF，
∵∠FBH=90°，
∴△BFH是等腰直角三角形，
∴FH=
BF，
∵FH=AF﹣AH=AF﹣CF，
∴AF﹣CF=BF，
∴AF=CF+BF．
①如图②中，结论：CF﹣AF=BF．
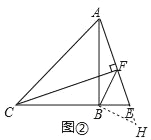
理由：作BH⊥BF交AF于H．
∵∠ABC=∠FBH，
∴∠FBC=∠ABH，
∵∠AFC=∠ABC=90°，
∴∠CEF+∠FCB=90°，∠AEB+∠BAH=90°
∴∠ECF=∠EAB，
在△BAH和△BCF中，
，
∴△BAH≌△BCF，
∴AH=CF，BH=BF，
∵∠FBH=90°，
∴△BFH是等腰直角三角形，
∴FH=BF，
∵FH=AH﹣AF=CF﹣AF，
∴CF﹣AF=BF．
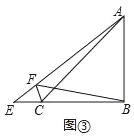
②如图③中，结论：CF+AF=BF．
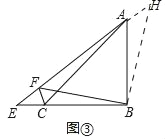
理由：作BH⊥BF交AF于H．
∵∠ABC=∠FBH，
∴∠FBC=∠ABH，
∵∠AFC=∠ABC=90°，
∴∠BCF+∠BAF=180°，∵∠BAF+∠BAH=180°
∴∠BCF=∠BAH，
在△BAH和△BCF中，
，
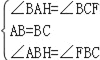∴△BAH≌△BCF，
∴AH=CF，BH=BF，
∵∠FBH=90°，
∴△BFH是等腰直角三角形，
∴FH=BF，
∵FH=AH+AF=CF+AF，
∴CF+AF=BF．
