Question

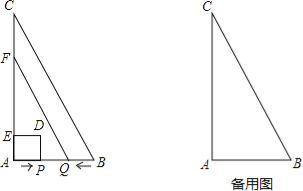
【题目】如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=2，CD=，点P在四边形ABCD的边上．若P到BD的距离为，则点P的个数为（ ）

A.1B.2C.3D.4

Answer 1

【答案】B

【解析】

首先作出AB、AD边上的点P（点A）到BD的垂线段AE，即点P到BD的最长距离，作出BC、CD的点P（点C）到BD的垂线段CF，即点P到BD的最长距离，由已知计算出AE、CF的长与比较得出答案．

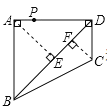过点A作AE⊥BD于E，过点C作CF⊥BD于F，

∵∠BAD=∠ADC=90°,AB=AD=2，CD=，

∴∠ABD=∠ADB=45°，

∴∠CDF=90°∠ADB=45°，

∵sin∠ABD=，

∴AE=ABsin∠ABD=2sin45

==2>，

所以在AB和AD边上有符合P到BD的距离为的点2个，

∵sin∠CDF=，

∴CF=CDsin∠CDF==1<，

所以在边BC和CD上没有到BD的距离为的点，

总之,P到BD的距离为的点有2个.

故选：B.