题目内容
1.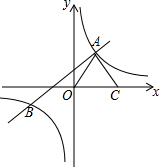 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3)、B(m,-1)两点.
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3)、B(m,-1)两点.(1)求直线和双曲线的解析式;
(2)观察图象,请直接写出不等式y=k1x+b>$\frac{{k}_{2}}{x}$的解集;
(3)点C为x轴正半轴上一点,连接AO、AC,且AO=AC,求S△AOC.
分析 (1)把A的坐标代入y=$\frac{{k}_{2}}{x}$即可求得双曲线的解析式,把B(m,-1)代入即可求得m,然后把A、B代入y=k1x+b,根据待定系数法即可求得直线的解析式;
(2)根据图象和A、B的坐标即可得出不等式y=k1x+b>$\frac{{k}_{2}}{x}$的解集;
(3)根据等腰三角形的性质和S△AOD=$\frac{1}{2}$|k|,即可求得.
解答 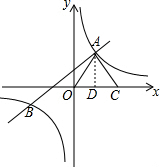 解:(1)∵双曲线y=$\frac{{k}_{2}}{x}$相经过点A(1,3),
解:(1)∵双曲线y=$\frac{{k}_{2}}{x}$相经过点A(1,3),
∴双曲线的解析式为:y=$\frac{3}{x}$.
∵点B(m,-1)在双曲线y=$\frac{3}{x}$ 上,
∴m=-3,则B点坐标为(-3,-1).
由点A(1,3),B(-3,-1)在直线y=k1x+b上,
得,$\left\{\begin{array}{l}{{k}_{1}+b=3}\\{-3{k}_{1}+b=-1}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{{k}_{1}=1}\\{b=2}\end{array}\right.$
∴直线的解析式为:y=x+2.
(2)由图可知,-3<x<0或x>1;
(3)过点A作AD⊥OC于点D,
∵AO=AC,
∴OD=DC,
∵点A在双曲线y=$\frac{3}{x}$图象上,
∴$\frac{1}{2}$OD•AD=$\frac{1}{2}$×3=$\frac{3}{2}$,
∴$\frac{1}{2}$CD•AD=$\frac{3}{2}$,
∴S△AOC=3.
点评 本题考查了待定系数法求反比例函数和一次函数的解析式,不等式的解集问题,以及三角形的面积,熟练掌握待定系数法是解题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
9.下列图形中,旋转120°后能与原图形重合的是( )
| A. | 等边三角形 | B. | 正方形 | C. | 正五边形 | D. | 正八边形 |
16.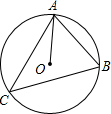 如图所示,⊙O是△ABC的外接圆,已知∠B=70°,则∠CAO的度数是( )
如图所示,⊙O是△ABC的外接圆,已知∠B=70°,则∠CAO的度数是( )
 如图所示,⊙O是△ABC的外接圆,已知∠B=70°,则∠CAO的度数是( )
如图所示,⊙O是△ABC的外接圆,已知∠B=70°,则∠CAO的度数是( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
13.下列四个实数中,是无理数的为( )
| A. | 0 | B. | $\sqrt{3}$ | C. | -1 | D. | $\frac{1}{3}$ |
10.-4的倒数是( )
| A. | 4 | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | 16 |
11.若(a+1)2+|2-b|=0,则ba的值为( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
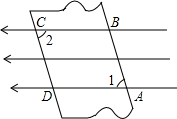 如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的∠1是72°15′,那么光线与纸板左上方所成的∠2是多少度?为什么?
如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的∠1是72°15′,那么光线与纸板左上方所成的∠2是多少度?为什么?