题目内容
若a、b是方程x2-3x+1=0的两个实数根,求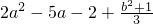 的值.
的值.
解:∵a、b是方程x2-3x+1=0的两个实数根,
∴a2-3a+1=0,b2-3b+1=0,
∴a2=3a-1,b2=3b-1,
∴原式=2(3a-1)-5a-2+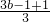
=a+b-4,
∵a、b是方程x2-3x+1=0的两个实数根,
∴a+b=3,
∴原式=3-4=-1.
分析:先根据方程的解得到a2-3a+1=0,b2-3b+1=0,变形后有a2=3a-1,b2=3b-1,再把它们代入原式得到原式=2(3a-1)-5a-2+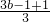 =a+b-4,然后根据根与系数的关系得到a+b=3,即可得到原式的值.
=a+b-4,然后根据根与系数的关系得到a+b=3,即可得到原式的值.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=- ,x1•x2=
,x1•x2= .也考查了一元二次方程的解.
.也考查了一元二次方程的解.
∴a2-3a+1=0,b2-3b+1=0,
∴a2=3a-1,b2=3b-1,
∴原式=2(3a-1)-5a-2+
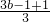
=a+b-4,
∵a、b是方程x2-3x+1=0的两个实数根,
∴a+b=3,
∴原式=3-4=-1.
分析:先根据方程的解得到a2-3a+1=0,b2-3b+1=0,变形后有a2=3a-1,b2=3b-1,再把它们代入原式得到原式=2(3a-1)-5a-2+
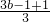 =a+b-4,然后根据根与系数的关系得到a+b=3,即可得到原式的值.
=a+b-4,然后根据根与系数的关系得到a+b=3,即可得到原式的值.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-
 ,x1•x2=
,x1•x2= .也考查了一元二次方程的解.
.也考查了一元二次方程的解. 
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目