题目内容
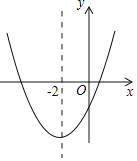
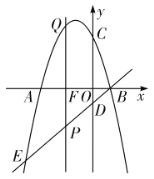
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() ,直线
,直线![]() 与抛物线交于点
与抛物线交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是线段
是线段![]() 上的一动点(不与
上的一动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() ,若
,若![]() ,线段
,线段![]() 是否存在最大值?若存在,请求出最大值,若不存在,请说明理由;
是否存在最大值?若存在,请求出最大值,若不存在,请说明理由;
(3)若![]() 轴上存在一点
轴上存在一点![]() ,使得
,使得![]() 时,求出点
时,求出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() 有最大值为
有最大值为![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为 或
或![]() .
.
【解析】
(1)确定抛物线解析式,关键是要确定抛物线经过的两点坐标,点![]() 是抛物线与
是抛物线与![]() 轴的交点,且位于
轴的交点,且位于![]() 轴上,因此易求出点
轴上,因此易求出点![]() 的坐标,再根据
的坐标,再根据![]() ,可求出点
,可求出点![]() ,
,![]() 的坐标,然后再将坐标代入两点式即可得解;
的坐标,然后再将坐标代入两点式即可得解;
(2)求出抛物线解析式后,利用![]() ,先求出点
,先求出点![]() 的横坐标,代入抛物线求出点
的横坐标,代入抛物线求出点![]() 的纵坐标,然后求出直线
的纵坐标,然后求出直线![]() 的解析式,最后再利用两函数解析式的纵坐标之差表示线段
的解析式,最后再利用两函数解析式的纵坐标之差表示线段![]() 长,进而在取值范围内求最值即可;
长,进而在取值范围内求最值即可;
(3)根据(2)中的直线解析式易知![]() ,由
,由![]() 可知
可知![]() ,则直线
,则直线![]() 上下两侧产生
上下两侧产生![]() 和
和![]() 的角,再利用锐角三角函数求出线段长,然后通过线段长转化为坐标即可.
的角,再利用锐角三角函数求出线段长,然后通过线段长转化为坐标即可.
解:(1)∵抛物线的解析式为![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴点![]() ,点
,点![]() .
.
设抛物线的解析式为![]() ,可得
,可得![]() ,
,
将点![]() 代入可得
代入可得![]() ,
,
∴抛物线解析式为![]() ;
;
(2)![]() 存在最大值.
存在最大值.
如解图①,过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() ,
,

∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() .
.
当![]() 时,
时,![]() ,
,
∴点![]() .
.
设直线BE的解析式为![]()
将点![]() 、
、![]() 代入解析式中得,
代入解析式中得,
![]() ,解得
,解得![]() .
.
∴直线![]() 的解析式为
的解析式为![]() .
.
设点![]() 的坐标为
的坐标为![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,
,
∴![]()
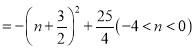
∴当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() ;
;
(3)分两种情况:①如解图①,当直线![]() 在直线
在直线![]() 的上方时,
的上方时,

∵点![]() 的坐标为
的坐标为![]() ,
,
∴![]() .
.
在直线![]() 中,当
中,当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为 ;
;
②如解图②,当直线![]() 在
在![]() 的下方时,
的下方时,

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
综上所述,点![]() 的坐标为
的坐标为 或
或![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?