题目内容
已知等边三角形ABC的边长为2,那么这个三角形的内切圆的半径为________.

分析:由等边三角形ABC的边长为2,根据等边三角形的性质与三角形内切圆的性质,即可求得答案.
解答:
 解:过O点作OD⊥AB,
解:过O点作OD⊥AB,∵O是等边△ABC的内心,
∴∠OAD=30°,
∵等边三角形ABC的边长为2,
∴OA=OB,
∴AD=
 AB=1,
AB=1,∴OD=AD•tan30°=
 .
.即这个三角形的内切圆的半径为:
 .
.故答案为:
 .
.点评:此题考查了三角形内切圆的性质以及等边三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目


 14、如图所示,已知等边三角形ABC的边长为 1,按图中所示的规律,用2011个这样的等边三角形镶嵌而成的四边形的周长是
14、如图所示,已知等边三角形ABC的边长为 1,按图中所示的规律,用2011个这样的等边三角形镶嵌而成的四边形的周长是
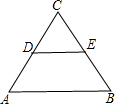 如图,已知等边三角形ABC的边长为2,DE是它的中位线,
如图,已知等边三角形ABC的边长为2,DE是它的中位线,