��Ŀ����
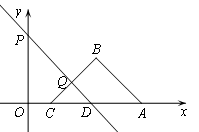
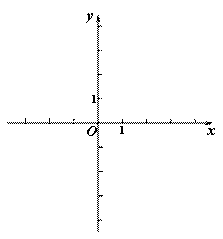
��ͼ����ƽ��ֱ�� ����ϵ�У��� A(5,0)��B(3,2)����C���߶�OA�ϣ�BC=BA����Q���߶�BC��һ�����㣬��P��������(0,3)��ֱ��PQ�Ľ���ʽΪy=kx+b(k��0)������x�ύ�ڵ�D��
����ϵ�У��� A(5,0)��B(3,2)����C���߶�OA�ϣ�BC=BA����Q���߶�BC��һ�����㣬��P��������(0,3)��ֱ��PQ�Ľ���ʽΪy=kx+b(k��0)������x�ύ�ڵ�D��
��1�����C�����꼰b��ֵ��
��2����k��ȡֵ��Χ��
��3����kΪȡֵ��Χ�ڵ��������ʱ������B��BE��x�ᣬ��PQ�ڵ�E����������y=ax2��5ax(a��0)�Ķ������ı���ABED���ڲ�����a��ȡֵ��Χ��
�⣺��1��ֱ��y=kx+b(k��0)����P(0,3)��
��b=3������������������������������������������1
 ����B��BF��AC��F��
����B��BF��AC��F��
��A(5,0)��B(3,2)��BC=BA��
���F�������ǣ�3,0����
���C�������ǣ�1,0������������������������������2
��2����ֱ��PC������Cʱ��k=��3��
��ֱ��PC������Bʱ��k= ��������������������3
��������������������3
�� ����������������������������������4
����������������������������������4
��3��
 ��k�����������k=��1��������������������������������������5
��k�����������k=��1��������������������������������������5
��ֱ��PQ�Ľ���ʽΪy=��x+3��
��������y=ax2��5ax(a��0)�Ķ��������� ���Գ���Ϊ
���Գ���Ϊ ��
��
�ⷽ���� ����
����
��ֱ��PQ��Գ���Ϊ �Ľ�������Ϊ
�Ľ�������Ϊ ����������������������������������6
����������������������������������6
�� ��
��
��� ������������������������������������������������������������7
������������������������������������������������������������7


 cm2 B.
cm2 B.  cm2 C. 6
cm2 C. 6 cm2 D��3
cm2 D��3
 ����ֻд��һ������
����ֻд��һ������
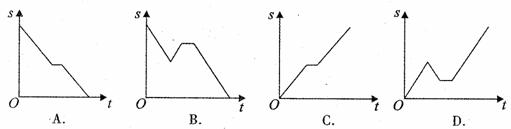
 B����һ��E����AEΪ����AB���Ϸ���������AENM����E��EF�ACD������ΪF�㣮��������AENM���ı���EFDB�������ȣ���AE�ij�Ϊ _��
B����һ��E����AEΪ����AB���Ϸ���������AENM����E��EF�ACD������ΪF�㣮��������AENM���ı���EFDB�������ȣ���AE�ij�Ϊ _��