题目内容
小兰和小潭分别用掷A、B两枚骰子的方法来确定P(x,y)的位置,她们规定:小兰掷得的点数为x,小谭掷得的点数为y,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为
- A.
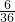
- B.

- C.

- D.

B
分析:列举出所有情况,看落在已知直线y=-2x+6上的情况占总情况的多少即可.
解答:列表得:

∴一共有36种情况,她们各掷一次所确定的点落在已知直线y=-2x+6上的有(1,4),(2,2).
∴她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为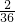 =
= .
.
故选B.
点评:列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;用到的知识点为:概率=所求情况数与总情况数之比;易错点是找到落在已知直线y=-2x+6上的情况数.
分析:列举出所有情况,看落在已知直线y=-2x+6上的情况占总情况的多少即可.
解答:列表得:

∴一共有36种情况,她们各掷一次所确定的点落在已知直线y=-2x+6上的有(1,4),(2,2).
∴她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为
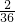 =
= .
.故选B.
点评:列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;用到的知识点为:概率=所求情况数与总情况数之比;易错点是找到落在已知直线y=-2x+6上的情况数.

练习册系列答案
相关题目
小兰和小潭分别用掷A、B两枚骰子的方法来确定P(x,y)的位置,她们规定:小兰掷得的点数为x,小谭掷得的点数为y,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
小兰和小潭分别用掷A、B两枚骰子的方法来确定P(x,y)的位置,她们规定:小兰掷得的点数为x,小谭掷得的点数为y,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
A.
B.
C.
D.
A.

B.

C.

D.

小兰和小潭分别用掷A、B两枚骰子的方法来确定P(x,y)的位置,她们规定:小兰掷得的点数为x,小谭掷得的点数为y,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
A.
B.
C.
D.
A.

B.

C.

D.








