Question

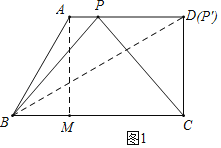
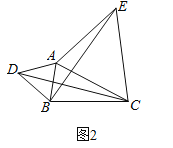
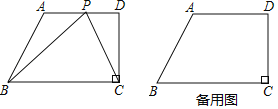
【题目】如图所示，在四边形ABCD中，AD∥BC，CD⊥BC，∠ABC＝60°，且AD＝12，BC＝18．动点P从点A出发，以每秒2个单位长度的速度向点D运动，设运动时间为t秒（0＜t≤6）

（1）当t＝6时，cos∠BPC＝　 　；

（2）当△BPC的外接圆与AD相切时，求t的值；

（3）在点P运动过程中，cos∠BPC是否存在最小值？若存在，请求出这个最小值；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）t＝；（3）存在，

【解析】

（1）过点A作AM⊥BC于M，证四边形AMCD为矩形，在Rt△ABM中求出AM的长度，推出CD的长度，在Rt△BDC中求出cos∠BDC的值即可；

（2）作BC的中垂线PH交BC于点H，交AD于点P'，连接BP'，CP'，作△BP'C的外接圆⊙O，则当点P运动到P'时，∴O与AD相切，求出此时t的值即可；

（3）连接PB，PC，设PB交⊙O于点N，连接NC，OB，先证明当动点P处于P’处时，∠BPC最大，则cos∠BPC的值最小，再证明∠BOH＝∠BP'C，求出此时cos∠BP'C的值即可．

解：（1）如图1，过点A作AM⊥BC于M，

∵CD⊥BC，

∴∠DCB＝∠AMC＝90°，

∵AD∥BC，

∴∠D＝180°﹣90°＝90°，

∴四边形AMCD为矩形，

∴AD＝MC＝12，

∴BM＝BC﹣MC＝6，

在Rt△ABM中，BM＝6，∠ABC＝60°，

∴AM＝BM＝6，

∴CD＝AM＝6，

当t＝6时，AP＝2t＝12，

∴点P与点D重合，

如图1，在Rt△BP'C中，P'C＝6，BC＝18，

∴BP'＝＝12，

∴cos∠BP'C＝＝；

故答案为：；

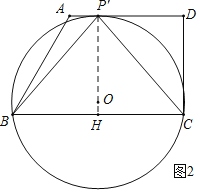
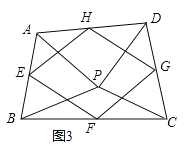
（2）如图2，作BC的中垂线PH交BC于点H，交AD于点P'，连接BP'，CP'，作△BP'C的外接圆⊙O，

则P'B＝P'C，圆心O在直线P'H上，

又∵AD∥BC，

∴P'H⊥AD，

∴当点P运动到P'时，∴O与AD相切，

∴∠DP'H＝∠P'HC＝∠HCD＝90°，

∴四边形P'HCD为矩形，

∴P'D＝HC＝BC＝9，

则AP'＝AD﹣P'D＝12﹣9＝3，

∴t＝，

∴当△BPC的外接圆与AD相切时，t＝；

（3）存在，

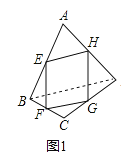
如图3，由（2）知，

当t＝秒时，△BPC的外接圆OO与AD相切于点P’

∵P'H＝DC＝6>BC＝9，

∴P'H>BH，

∴∠BP'C<90°，圆心O在弦BC的上方，P是AD上一动点，

连接PB，PC，设PB交⊙O于点N，连接NC，

则∠BP'C＝∠BNC≥∠BPC，

∴当动点P处于P’处时，∠BPC最大，则cos∠BPC的值最小，

此时，连接OB，则∠BOH＝2∠BP'H＝∠BP'C，

由题意，知OB＝OP'＝P'H﹣OH＝6﹣OH，

在Rt△BOH中，OH2+BH2＝OB2，

∴OH2+92＝（6﹣OH）2，

解得，OH＝，

∴OB＝6﹣OH＝，

在Rt△BOH中，

cos∠BOH＝＝，

∵∠BOH＝∠BP'C，

∴cos∠BPC的值最小为．