题目内容
如图，点A、C都在函数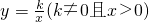
的图象上，点B、D都在x轴上，使得△OAB、△BCD都
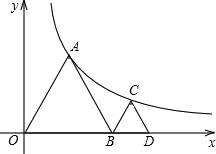是等边三角形，且点D的坐标为（4，0），则K=________．
2
分析：根据等边三角形的性质得出AN，AM，ZC，CF的长，再利用反比例函数的性质得出即可．
解答：作AM⊥BO，AN⊥y轴，CF⊥BD，CZ⊥ON，假设BO=2x，
∵△OAB、△BCD都是等边三角形，且点D的坐标为（4，0），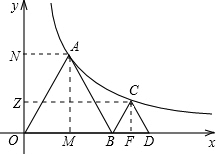
∴MO=x，AM=x，
∴ZC=4-
=2+x，CF=（2-x），
∴K=AN×AM=ZC×CF，
∴x2=（2-x）（2+x），
解得：x2=2，
∴K=x2=2，
故答案为：2．
点评：此题主要考查了反比例函数的性质以及等边三角形的性质，根据已知表示出AN，AM，ZC，CF的长是解决问题的关键．
分析：根据等边三角形的性质得出AN，AM，ZC，CF的长，再利用反比例函数的性质得出即可．
解答：作AM⊥BO，AN⊥y轴，CF⊥BD，CZ⊥ON，假设BO=2x，
∵△OAB、△BCD都是等边三角形，且点D的坐标为（4，0），
∴MO=x，AM=
x，∴ZC=4-
=2+x，CF=（2-x），∴K=AN×AM=ZC×CF，
∴
x2=（2-x）（2+x），解得：x2=2，
∴K=
x2=2，故答案为：2
．点评：此题主要考查了反比例函数的性质以及等边三角形的性质，根据已知表示出AN，AM，ZC，CF的长是解决问题的关键．
练习册系列答案
相关题目
25、（1）已知二次函数y=ax2+bx+c（a≠0）的图象开口向下，并经过点（-1，2），（1，0）．下列命题其中一定正确的是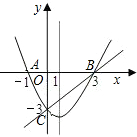
如图，在同一直角坐标系中，二次函数的图象与两坐标轴分别交于A（-1，0）、点B（3，0）和点C（0，-3），一次函数的图象与抛物线交于B、C两点．
如图，在同一坐标系内，二次函数的图象与两坐标轴分别交于点A（-1，0），点B（2，0）和点C（0，4），一次函数的图象与抛物线交于B，C两点．
（2012•相城区一模）如图，已知正比例函数和反比例函数的图象都经过点M（-2，-1），且P（-1，-2）为双曲线上的一点．
如图，直线l1的解析表达式为y=x+1，且l1与x轴交于点B（-1，0），与y轴交于点D．l2与y轴的交点为C（0，-3），直线l1、l2相交于点A（2，3），结合图象解答下列问题：