题目内容
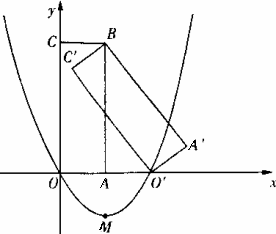
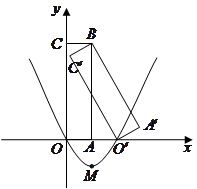
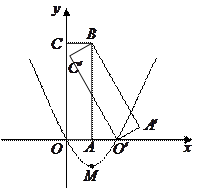
如图,矩形 是矩形
是矩形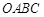 (边
(边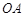 在
在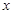 轴正半轴上,边
轴正半轴上,边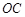 在
在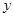 轴正半
轴正半
轴上)绕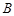 点逆时针旋转得到的,
点逆时针旋转得到的,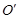 点在
点在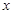 轴的正半轴上,
轴的正半轴上,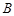 点的坐标为
点的坐标为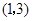 .
.

(1)如果二次函数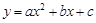 (
(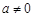 )的图象经过
)的图象经过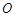 ,
,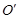 两点且图象顶点
两点且图象顶点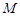 的纵坐标为
的纵坐标为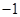 ,求这个二次函数的解析式;
,求这个二次函数的解析式;
(2)在(1)中求出的二次函数图象对称轴的右支上是否存在点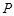 ,使得
,使得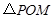 为直角三角形?若存在,请求出
为直角三角形?若存在,请求出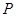 点的坐标和
点的坐标和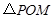 的面积;若不存在,请说明理由;
的面积;若不存在,请说明理由;
(3)求边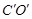 所在直线的解析式.
所在直线的解析式.
【答案】
解:(1)连结 ,
,

则



 ,
,
 解得
解得 ,
, ,
,
 所求二次函数的解析式为
所求二次函数的解析式为
(2)设存在满足题设条件的点 连结
连结 ,
, ,
, ,过
,过 作
作 轴于
轴于
则 ,
, ,
, ,
,

 ,
, 即
即
 在二次函数
在二次函数 的图象上
的图象上
 解得
解得 或
或
 在对称轴的右支上
在对称轴的右支上 


即 是所求的点 连结
是所求的点 连结 ,显然
,显然 为等腰直角三角形.
为等腰直角三角形.
 为满足条件的点
为满足条件的点
 满足条件的点是
满足条件的点是 或
或
 ,
,
 或
或
(3)设 与
与 的交点为
的交点为 ,显然
,显然
在 中,
中, ,即
,即 解得
解得

设边 所在直线的解析式为
所在直线的解析式为 ,则
,则
解得 ,
,
 所求直线解析式为
所求直线解析式为
【解析】略

练习册系列答案
相关题目
 ,使得
,使得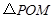 为直角三角形?若存在,请求出
为直角三角形?若存在,请求出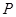 点的坐标和
点的坐标和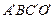 是矩形
是矩形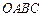 (边
(边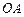 在
在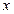 轴正半轴上,边
轴正半轴上,边 在
在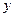 轴正半
轴正半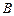 点逆时针旋转得到的,
点逆时针旋转得到的, 点在
点在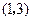 .
.
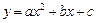 (
(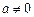 )的图象经过
)的图象经过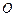 ,
, 的纵坐标为
的纵坐标为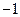 ,求这个二次函数的解析式;
,求这个二次函数的解析式;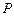 ,使得
,使得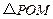 为直角三角形?若存在,请求出
为直角三角形?若存在,请求出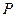 点的坐标和
点的坐标和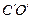 所在直线的解析式.
所在直线的解析式. 是矩形
是矩形 (边
(边 在
在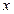 轴正半轴上,边
轴正半轴上,边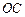 在
在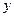 轴正半
轴正半
 点逆时针旋转得到的,
点逆时针旋转得到的,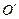 点在
点在 .
.
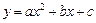 (
(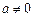 )的图象经过
)的图象经过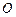 ,
,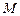 的纵坐标为
的纵坐标为 ,求这个二次函数的解析式;
,求这个二次函数的解析式; ,使得
,使得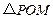 为直角三角形?若存在,请求出
为直角三角形?若存在,请求出 点的坐标和
点的坐标和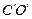 所在直线的解析式.
所在直线的解析式.