题目内容
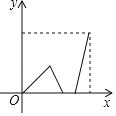
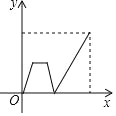
【题目】如图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为_____.

【答案】114゜
【解析】
如图,设∠B′FE=x,根据折叠的性质得∠BFE=∠B′FE=x,∠AEF=∠A′EF,则∠BFC=x18°,再由第2次折叠得到∠C′FB=∠BFC=x18°,于是利用平角定义可计算出x=66°,接着根据平行线的性质得∠A′EF=180°∠B′FE=114°,所以∠AEF=114°.
解:如图,设∠B′FE=x,
∵纸条沿EF折叠,
∴∠BFE=∠B′FE=x,∠AEF=∠A′EF,
∴∠BFC=∠BFE﹣∠CFE=x﹣18°,
∵纸条沿BF折叠,
∴∠C′FB=∠BFC=x﹣18°,
而∠B′FE+∠BFE+∠C′FE=180°,
∴x+x+x﹣18°=180°,解得x=66°,
∵A′D′∥B′C′,
∴∠A′EF=180°﹣∠B′FE=180°﹣66°=114°,
∴∠AEF=114°.
故答案为:114°.


练习册系列答案
相关题目