题目内容
如图,点P是反比例函数 图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=
图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=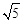 。
。
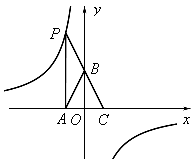
(1)k的值是 ;
(2)若M(a,b)是该反比例函数图象上的点,且满足∠MBA<∠ABC,则a的取值范围是 。
 图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=
图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=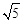 。
。
(1)k的值是 ;
(2)若M(a,b)是该反比例函数图象上的点,且满足∠MBA<∠ABC,则a的取值范围是 。
(1) ;(2)0<a<2或
;(2)0<a<2或 。
。
 ;(2)0<a<2或
;(2)0<a<2或 。
。(1)依题意,AO=1,OC=1,∴AB是Rt△PAC斜边上的中线。
∵AB=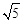 ,∴PC=
,∴PC= 。
。
∴在Rt△PAC中,AC=2,AP= ,PC=
,PC= ,
,
∴根据勾股定理,得: ,解得
,解得 。
。
∵ ,∴
,∴ 。
。
(2)分两种情况:
①当点M在x轴下方时,考虑∠MBA=∠ABC的情况:当∠MBA=∠ABC时,点M是PC与双曲线的另一个交点,由B(0,2),C(1,0)易得直线PC的解析式为 ,与
,与 联立:
联立:
 ,解得:
,解得: 或
或 (点P坐标,舍去),
(点P坐标,舍去),
∴当∠MBA=∠ABC时,点M的坐标为(2,-2)。
∴当∠MBA<∠ABC时,0<a<2。
②当点M在x轴上方时,考虑∠MBA=∠ABC的情况:如图,将△ABC顺时针旋转至
△EBA,延长BE交 于点
于点 ,则
,则 之间横坐标的值即为所求。过点E分别作x轴和y轴的垂线,垂足分别为点F,G,设点E的坐标为(x,y),
之间横坐标的值即为所求。过点E分别作x轴和y轴的垂线,垂足分别为点F,G,设点E的坐标为(x,y),

由旋转的性质,得AE=AC=2,BE=BA=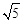 。
。
在Rt△AEF中,由勾股定理,得 ,即
,即 ①,
①,
在Rt△BEG中,由勾股定理,得 ,即
,即 ②,
②,
①-②,得 ,即
,即 ③,
③,
将③代入②,得 ,解得
,解得 或
或 (舍去),
(舍去),
将 代入③得
代入③得 。
。
∴点E的坐标为 。
。
设直线BE的解析式为 ,则
,则 。
。
∴直线BE的解析式为 。
。
联立 。
。
∴ 。
。
综上所述,a的取值范围是0<a<2或 。
。
∵AB=
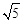 ,∴PC=
,∴PC= 。
。∴在Rt△PAC中,AC=2,AP=
 ,PC=
,PC= ,
, ∴根据勾股定理,得:
 ,解得
,解得 。
。∵
 ,∴
,∴ 。
。(2)分两种情况:
①当点M在x轴下方时,考虑∠MBA=∠ABC的情况:当∠MBA=∠ABC时,点M是PC与双曲线的另一个交点,由B(0,2),C(1,0)易得直线PC的解析式为
 ,与
,与 联立:
联立: ,解得:
,解得: 或
或 (点P坐标,舍去),
(点P坐标,舍去),∴当∠MBA=∠ABC时,点M的坐标为(2,-2)。
∴当∠MBA<∠ABC时,0<a<2。
②当点M在x轴上方时,考虑∠MBA=∠ABC的情况:如图,将△ABC顺时针旋转至
△EBA,延长BE交
 于点
于点 ,则
,则 之间横坐标的值即为所求。过点E分别作x轴和y轴的垂线,垂足分别为点F,G,设点E的坐标为(x,y),
之间横坐标的值即为所求。过点E分别作x轴和y轴的垂线,垂足分别为点F,G,设点E的坐标为(x,y),
由旋转的性质,得AE=AC=2,BE=BA=
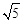 。
。在Rt△AEF中,由勾股定理,得
 ,即
,即 ①,
①,在Rt△BEG中,由勾股定理,得
 ,即
,即 ②,
②,①-②,得
 ,即
,即 ③,
③,将③代入②,得
 ,解得
,解得 或
或 (舍去),
(舍去),将
 代入③得
代入③得 。
。∴点E的坐标为
 。
。设直线BE的解析式为
 ,则
,则 。
。∴直线BE的解析式为
 。
。联立
 。
。∴
 。
。综上所述,a的取值范围是0<a<2或
 。
。
练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

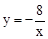 的图象与线段AB交于M点,且AM=BM.
的图象与线段AB交于M点,且AM=BM.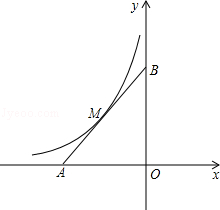
 (x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
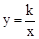 的图象经过点C,一次函数
的图象经过点C,一次函数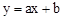 的图象经过点C,一次函数
的图象经过点C,一次函数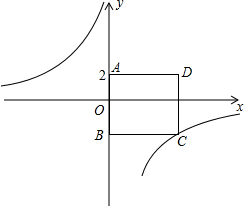
 与反比例函数
与反比例函数 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(-1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(-1,m).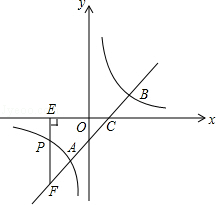
 的图象经过点(-1,-2),则k的值是( ).
的图象经过点(-1,-2),则k的值是( ). 的顶点
的顶点 的坐标为
的坐标为 ,顶点
,顶点 在
在 轴的正半轴上.反比例函数
轴的正半轴上.反比例函数 的图象经过顶点
的图象经过顶点 ,则
,则 的值为( )
的值为( ) 
 的图象在第一象限内交于点B,点C是函数
的图象在第一象限内交于点B,点C是函数