题目内容
一艘渔船正以30海里/时，的速度由西向东追赶鱼群，在A处看见小岛C在船北偏东60°的方向上，40min后渔船行驶到B处，此时小岛C在船北偏东30°的方向上，继续向东走则船与小岛之间最短距离为分析：由已知画出图形，在A处看见小岛C在船北偏东60°的方向上，得到∠DAC=30°，小岛C在船北偏东30°的方向上，得到∠DBC=60°，还可以得出∠ACB=30°，所以AB=BC，再利用三角函数关系求出CD．
解答：
解：过点C作CD⊥AD，垂足为D，
由题意得：
∵∠DAC=30°，∠DBC=60°，
∴∠ACB=30°，
∴AB=BC，
又∵渔船速度30海里/时，40min航行20海里，即AB=BC=20海里，
cos30°=
=
=
，
解得：CD=10
海里．
故答案为：10
．
解：过点C作CD⊥AD，垂足为D，由题意得：
∵∠DAC=30°，∠DBC=60°，
∴∠ACB=30°，
∴AB=BC，
又∵渔船速度30海里/时，40min航行20海里，即AB=BC=20海里，
cos30°=
| CD |
| BC |
| CD |
| 20 |
| ||
| 2 |
解得：CD=10
| 3 |
故答案为：10
| 3 |
点评：此题主要考查了解直角三角形中，由已知如何画出图形，并由已知发现隐含条件，题目比较典型．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
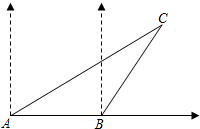如图，一艘渔船正以30海里/小时的速度由西向东赶鱼群，在A处看风小岛C在船的北偏东60度．40分钟后，渔船行至B处，此时看见小岛C在船的北偏东30度．已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区，问这艘渔船继续向东追赶鱼群，是否有进入危险区的可能？
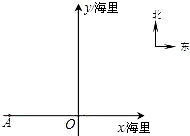分钟后，渔船行至O处，此时看见小岛B在船的北偏东30°．在如图所示的坐标系中，点O为坐标原点，点A位于x轴上．
