题目内容
小明在解方程| 1 |
| x-2 |
| 1 |
| x-4 |
| 1 |
| x-3 |
| 1 |
| x-5 |
| 7 |
| 2 |
| 1 |
| x-7 |
| 1 |
| x-5 |
| 1 |
| x-6 |
| 1 |
| x-4 |
| 11 |
| 2 |
| 1 |
| x-7 |
| 1 |
| x-3 |
| 1 |
| x-6 |
| 1 |
| x-2 |
| 1 |
| x-a |
| 1 |
| x-b |
| 1 |
| x-c |
| 1 |
| x-d |
分析:先根据解分式方程的步骤求出方程
-
=
-
的解,然后观察找出规律:方程的解正好等于7+3+6+2之和的四分之一,又因为7+2=6+3,所以方程的解x=
=
,因此方程
-
=
-
的解x=
=
.
| 1 |
| x-7 |
| 1 |
| x-3 |
| 1 |
| x-6 |
| 1 |
| x-2 |
| 7+2 |
| 2 |
| 6+3 |
| 2 |
| 1 |
| x-a |
| 1 |
| x-b |
| 1 |
| x-c |
| 1 |
| x-d |
| a+d |
| 2 |
| b+c |
| 2 |
解答:解:方程
-
=
-
两边通分得:
=
,
=
,
(x-7)(x-3)=(x-6)(x-2),
x2-10x+21=x2-8x+12,
解得x=
;
经检验x=
是元方程的解.
观察方程
-
=
-
可得:x=
=
=
,
所以方程
-
=
-
的解为:x=
=
.
| 1 |
| x-7 |
| 1 |
| x-3 |
| 1 |
| x-6 |
| 1 |
| x-2 |
| x-3-x+7 |
| (x-7)(x-3) |
| x-2-x+6 |
| (x-6)(x-2) |
| 4 |
| (x-7)(x-3) |
| 4 |
| (x-6)(x-2) |
(x-7)(x-3)=(x-6)(x-2),
x2-10x+21=x2-8x+12,
解得x=
| 9 |
| 2 |
经检验x=
| 9 |
| 2 |
观察方程
| 1 |
| x-7 |
| 1 |
| x-3 |
| 1 |
| x-6 |
| 1 |
| x-2 |
| 9 |
| 2 |
| 7+2 |
| 2 |
| 6+3 |
| 2 |
所以方程
| 1 |
| x-a |
| 1 |
| x-b |
| 1 |
| x-c |
| 1 |
| x-d |
| a+d |
| 2 |
| b+c |
| 2 |
点评:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.
(2)解分式方程一定注意要验根.

练习册系列答案
相关题目
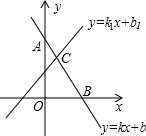 在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:
在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:一次函数与方程的关系:
| (1)一次函数的解析式就是一个二元一次方程; (2)点B的横坐标是方程①的解; (3)点C的坐标(x,y)中的x,y的值是方程组②的解.一次函数与不等式的关系;
|
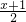 >2x+1
>2x+1