Question

矩形ABCD中，AB＝8，BC＝3 ，点P在边AB上，且BP＝3AP，如果圆P是以点P为圆心，PD为半径的圆，那么下列判断正确的是（    ）

A．点B、C均在圆P外

B．点B在圆P外、点C在圆P内

C．点B在圆P内、点C在圆P外

D．点B、C均在圆P内

Answer 1

C

解析试题分析：
∵AB=8，点P在边AB上，且BP=3AP
∴AP=2，
∴根据勾股定理得出，r=PD=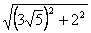=7，PC=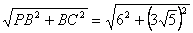==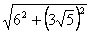9，
∵PB=6＜r，PC=9＞r
∴点B在圆P内、点C在圆P外,故选C．
考点：点与圆的位置关系的判定
点评：难度系数中等，此题应根据点与圆心之间的距离和圆的半径的大小关系作出判断