��Ŀ����
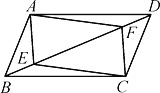
����Ŀ�� ��ͼ����ƽ��ֱ������ϵ�У���A������Ϊ��6��![]() ����AB��x���ڵ�B��AC��y���ڵ�C������BC����D���߶�AC���е㣬��E������Ϊ��0��
����AB��x���ڵ�B��AC��y���ڵ�C������BC����D���߶�AC���е㣬��E������Ϊ��0��![]() ������F���߶�EO�ϵ�һ�����㣮����A��D��F����������x�������ύ�ڵ�G������DG���߶�AB�ڵ�M��
������F���߶�EO�ϵ�һ�����㣮����A��D��F����������x�������ύ�ڵ�G������DG���߶�AB�ڵ�M��
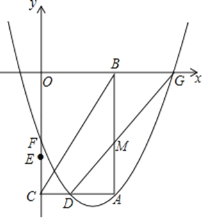
(1)���ACB�Ķ�����
(2)����F�˶���ԭ��ʱ�����A��D��F����������ߵĺ�������ʽ����G�����ꣻ
(3)���߶�DMΪһ�����ȱ�������DMP����P���A��ֱ��DGͬ�࣬����F�ӵ�E�˶�����Oʱ����ֱ��д����P�˶���·���ij���
���𰸡�(1)![]() (2)
(2)![]()
![]() (3)
(3)![]()
��������
��1����ȷ����AB��AC�����жϳ���BAC��90�㣬�����������Ǻ������ɵó����ۣ�
��2����ȷ������C�����꣬����ȷ������D�����꣬����ô���ϵ���������ɵó����ۣ�
��3�����жϳ���F�ӵ�E�˶�����Oʱ����M���˶��켣��MM'�������жϳ���P���˶��켣�����жϳ���MDM'�ա�PDP'�����ֱ��BG�Ľ���ʽ�����������M�����꣬���ɵó����ۣ�
�⣺��1���ߵ�A������Ϊ![]() ��AB��x���ڵ�B��
��AB��x���ڵ�B��
��B��6��0����
��AB��![]() ��
��
�ߵ�A������Ϊ![]() ��AC��y���ڵ�C��
��AC��y���ڵ�C��
��C��0��![]() ����
����
��AC��6��
��AB��x�ᣬAC��y�ᣬ
���ABO����ACO��90�㣽��BOC��
���ı���OBAC�Ǿ��Σ�
���BAC��90�㣬
��Rt��ABC��tan��ACB��![]() ��
��
���ACB��60�㣻
��2���ɣ�1��֪��C��0��![]() ����
����
�ߵ�D��AC���е㣬
��D��3��![]() ����
����
�������ߵĽ���ʽΪy��ax2+bx+c��
����A��6��![]() ����D��3��
����D��3��![]() ����O��0��0�����������߽���ʽ�У���
����O��0��0�����������߽���ʽ�У���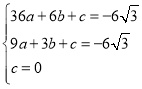 ��
��
��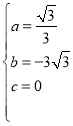 ��
��
�������ߵĽ���ʽΪ![]() ��
��
��y��0����![]() ��
��
��x��0��x��9��
��G��9��0����
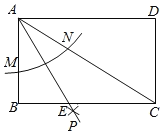
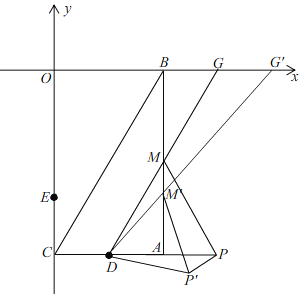
��3����ͼ��
����F�ӵ�E�˶�����Oʱ����M���˶��켣���߶�MM'��
����DMΪ�ߵĵȱ������εĶ���P�Ĺ켣���߶�PP'��
�������߹�ԭ��ʱ��DG��AB�Ľ��������M���������߹���Eʱ��DG'��AB�Ľ���ΪM'��
�ߡ�DMP�ǵȱ������Σ�
��DM��DP����MDP��60�㣬
�ߡ�DM'P'�ǵȱ�������
��DM'��DP'����M'DP'��60�㣬
���MDM'����PDP'��
���MDM'�ա�PDP'��SAS����
��PP'��MM'��
�ɣ�2��֪��G��9��0����
��D��3��![]() ����
����
��ֱ��DG�Ľ���ʽ![]() ��
��
��x��6����y��![]() ��
��
��M![]() ��
��
�������߹���Eʱ���������߹���A��D��E��
�������ߵĽ���ʽΪ![]() ��
��
��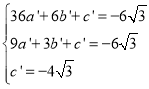 ��
��
��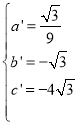 ��
��
�����A��D��E�������ߵĽ���ʽΪ![]() ��
��
��y��0����![]() ��
��
��x����3��x��12��
��G'��12��0����
��DG'�Ľ���ʽΪ![]() ��
��
��x��6����y��![]() ��
��
��M'��6��![]() ����
����
��PP'��MM'��![]() ��
��
����P�˶���·���ij�Ϊ![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�