题目内容
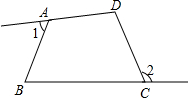如图在四边形ABCD中，∠1和∠2分别是∠A和∠C的外角，且∠B+∠D=140°，则∠1+∠2=________°．
140
分析：利用四边形内角和定理求得∠DAB+∠DCB，然后利用邻补角的定义即可求解．
解答：∵∠DAB+∠DCB=360°-（∠B+∠D）=360°-140°=220°
∴∠1+∠2=2×180°-（∠DAB+∠DCB）=360°-220°=140°．
故答案是：140°．
点评：本题考查了四边形的内角和定理以及邻补角的定义，正确理解∠1+∠2=2×180°-（∠DAB+∠DCB）是关键．
分析：利用四边形内角和定理求得∠DAB+∠DCB，然后利用邻补角的定义即可求解．
解答：∵∠DAB+∠DCB=360°-（∠B+∠D）=360°-140°=220°
∴∠1+∠2=2×180°-（∠DAB+∠DCB）=360°-220°=140°．
故答案是：140°．
点评：本题考查了四边形的内角和定理以及邻补角的定义，正确理解∠1+∠2=2×180°-（∠DAB+∠DCB）是关键．
练习册系列答案
相关题目
22、已知：如图在四边形ABCD中，∠A=∠D、∠B=∠C，试判断AD与BC的位置关系，并说明理由．
如图在四边形ABCD中，E是对角线BD上一点，EF∥AD，EM∥BC，则
如图在四边形ABCD中，∠ACB+∠ADB=180°，∠ABC=∠BAC=60°．
如图在四边形ABCD中，∠1和∠2分别是∠A和∠C的外角，且∠B+∠D=140°，则∠1+∠2=
度数？如果能请求出∠A的度数，如果不能请补充一个条件使其能求出∠A的度数，请完善解题过程