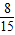题目内容
(新颖题)△ABC∽△A1B1C1,且相似比为
,△A1B1C1∽△A2B2C2,且相似比为
,则△ABC与△A2B2C2的相似比为( )
| 2 |
| 3 |
| 5 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:利用两组相似三角形的相似比,进行转化即可得出,其实相乘即可.
解答:解:∵△ABC∽△A1B1C1,相似比为
=
,
又∵△A1B1C1∽△A2B2C2,相似比为
=
,
∴△ABC与△A2B2C2的相似比为
=
.
故选A.
| 2 |
| 3 |
| 10 |
| 15 |
又∵△A1B1C1∽△A2B2C2,相似比为
| 5 |
| 4 |
| 15 |
| 12 |
∴△ABC与△A2B2C2的相似比为
| 10 |
| 12 |
| 5 |
| 6 |
故选A.
点评:本题考查了相似三角形的传递性,也可以用其他方法解.

练习册系列答案
相关题目
 ,△A1B1C1∽△A2B2C2,且相似比为
,△A1B1C1∽△A2B2C2,且相似比为 ,则△ABC与△A2B2C2的相似比为( )
,则△ABC与△A2B2C2的相似比为( )

 或
或
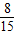
 ,△A1B1C1∽△A2B2C2,且相似比为
,△A1B1C1∽△A2B2C2,且相似比为 ,则△ABC与△A2B2C2的相似比为( )
,则△ABC与△A2B2C2的相似比为( )

 或
或
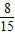
 ,△A1B1C1∽△A2B2C2,且相似比为
,△A1B1C1∽△A2B2C2,且相似比为 ,则△ABC与△A2B2C2的相似比为( )
,则△ABC与△A2B2C2的相似比为( )

 或
或