题目内容
3.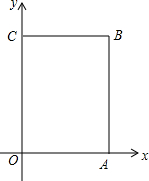 已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动).
已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动).(1)写出B点的坐标((4,6));
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
分析 (1)根据矩形的对边相等,可得CB,AB的长,根据点的坐标表示方法,可得答案;
(2)根据速度乘时间等于路程,可得OA+AP的长度,根据点的坐标表示方法,可得答案;
(3)分类讨论:①OA+AP=9=2t,②OA+AB+BC+CP=4+6+4+6-5=2t,根据解方程,可得答案.
解答 解:(1)由矩形的性质,得
CB=OA=4,AB=OC=6,
B(4,6);
故答案为:(4,6);
(2)由每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动),
点P移动了4秒,得P点移动了8个单位,即OA+AP=8,
P点在AB上且距A点4个单位,
P(4,4);
(3)第一次距x轴5个单位时AP=5,即OA+AP=9=2t,
解得t=$\frac{9}{2}$,
第二次距x轴5个单位时,OP=5,即 OA+AB+BC+CP=4+6+4+6-5=2t,解得t=$\frac{15}{2}$,
综上所述:t=$\frac{9}{2}$秒,或t=$\frac{15}{2}$秒时,点P到x轴的距离为5个单位长度.
点评 本题考查了坐标与图形的性质,利用了矩形的性质,点的坐标的表述方法,利用速度乘时间等于路程得出关于t的方程是解题关键,分类讨论是解题关键.

练习册系列答案
相关题目
11.方程2x-1=5的解是( )
| A. | x=3 | B. | x=2 | C. | x=-3 | D. | x=-2 |

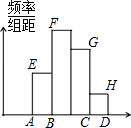 某校七年级在“数学小论文”评比活动中,共征集到论文30篇,并对其进行评比、整理,分成组画出频数分布直方图(如图),从左到右各小长方形的高度比为2:4:3:1,则第2组的频数为( )
某校七年级在“数学小论文”评比活动中,共征集到论文30篇,并对其进行评比、整理,分成组画出频数分布直方图(如图),从左到右各小长方形的高度比为2:4:3:1,则第2组的频数为( )