题目内容
12.计算1+4+9+16+25+…的前29项的和是8555.分析 根据每一项分别是12、22、32、42、52可找到规律,整理可得原式关于n的一个函数式,即可解题.
解答 解:12+22+32+42+52+…+292+…+n2
=0×1+1+1×2+2+2×3+3+3×4+4+4×5+5+…(n-1)n+n
=(1+2+3+4+5+…+n)+[0×1+1×2+2×3+3×4+…+(n-1)n]
=$\frac{n(n+1)}{2}$+{$\frac{1}{3}$(1×2×3-0×1×2)+$\frac{1}{3}$(2×3×4-1×2×3)+$\frac{1}{3}$(3×4×5-2×3×4)+…+$\frac{1}{3}$[(n-1)•n•(n+1)-(n-2)•(n-1)•n]}
=$\frac{n(n+1)}{2}$+$\frac{1}{3}$[(n-1)•n•(n+1)]
=$\frac{n(n+1)(2n+1)}{6}$,
∴当n=29时,原式=$\frac{29×(29+1)×(2×29+1)}{6}$=8555.
故答案为 8555.
点评 本题考查了学生发现规律并且整理的能力,本题中整理出原式关于n的解析式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.由于受H7N9禽流感的影响,我市某城区今年2月份鸡的价格比1月份下降a%,3月份比2月份下降b%,已知1月份鸡的价格为24元/千克.设3月份鸡的价格为m元/千克,则( )
| A. | m=24(1-a%-b%) | B. | m=24(1-a%)b% | C. | m=24-a%-b% | D. | m=24(1-a%)(1-b%) |
4. 如图,一条公路第一次转弯转的角∠β=140°,若使两次转变后回到原来的方向,∠C应是( )
如图,一条公路第一次转弯转的角∠β=140°,若使两次转变后回到原来的方向,∠C应是( )
 如图,一条公路第一次转弯转的角∠β=140°,若使两次转变后回到原来的方向,∠C应是( )
如图,一条公路第一次转弯转的角∠β=140°,若使两次转变后回到原来的方向,∠C应是( )| A. | 140° | B. | 40° | C. | 100° | D. | 180° |
1. 如图,与∠1是同位角的为( )
如图,与∠1是同位角的为( )
 如图,与∠1是同位角的为( )
如图,与∠1是同位角的为( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
2.下列说法中,正确的是( )
| A. | 若a≠b,则a2≠b2 | B. | 若a>|b|,则a>b | C. | 若|a|=|b|,则a=b | D. | 若|a|>|b|,则a>b |
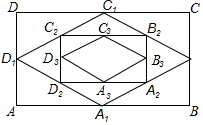 由四边形四条边的中点组成的四边形叫做原四边形的中点四边形.如图,四边形ABCD是矩形,取矩形ABCD四条边的中点得到中点四边形A1B1C1D1,再取四边形A1B1C1D1四条边的中点得到中点四边形A2B2C2D2,…,按此规律继续下去,若矩形ABCD的面积为1,则得到的中点四边形AnBnCnDn的面积为$\frac{1}{{2}^{n}}$.
由四边形四条边的中点组成的四边形叫做原四边形的中点四边形.如图,四边形ABCD是矩形,取矩形ABCD四条边的中点得到中点四边形A1B1C1D1,再取四边形A1B1C1D1四条边的中点得到中点四边形A2B2C2D2,…,按此规律继续下去,若矩形ABCD的面积为1,则得到的中点四边形AnBnCnDn的面积为$\frac{1}{{2}^{n}}$. 如图,AB=AC,且AB⊥AC,若C(0,-1),B(-4,0),求点A坐标.
如图,AB=AC,且AB⊥AC,若C(0,-1),B(-4,0),求点A坐标.