题目内容
如图，⊙O和⊙O1分别是△ABC的外接圆和内切圆，两圆的半径分别为6和2，连接AO1并延长交⊙O于D，则AO1•O1D的值为（ ）| A、24 | B、12 | C、16 | D、20 |
分析：过D作圆O的直径DQ，连接QC、DC、O1E、BO1、BD，由圆周角定理求出∠DEC=∠DAC，∠DCQ=90°，证△AO1E∽△QDC，得到
=
，求出AO1•DC=24，根据三角形的内切圆和三角形的外角性质推出∠DBO1=∠BO1D，推出O1D=BD=CD，即可求出答案．
| AO1 |
| DQ |
| O1E |
| DC |
解答：
解：过D作圆O的直径DQ，连接QC、DC、O1E、BO1、BD，
∠DEC=∠DAC，∠DCQ=90°，
∵O1E⊥AC，
∴∠AEO1=90°=∠DQC，
∴△AO1E∽△QDC，
∴
=
，
AO1•DC=2×（6+6）=24，
∵圆O1是△ABC的内切圆，
∴∠BAD=∠DAC，∠ABO1=∠CBO1，弧BD=弧CD，
∴∠DBO1=∠BO1D，DB=CD，
∴O1D=BD=CD，
∴AO1•O1D=24，
故选A．
解：过D作圆O的直径DQ，连接QC、DC、O1E、BO1、BD，∠DEC=∠DAC，∠DCQ=90°，
∵O1E⊥AC，
∴∠AEO1=90°=∠DQC，
∴△AO1E∽△QDC，
∴
| AO1 |
| DQ |
| O1E |
| DC |
AO1•DC=2×（6+6）=24，
∵圆O1是△ABC的内切圆，
∴∠BAD=∠DAC，∠ABO1=∠CBO1，弧BD=弧CD，
∴∠DBO1=∠BO1D，DB=CD，
∴O1D=BD=CD，
∴AO1•O1D=24，
故选A．
点评：本题主要考查对三角形的外角性质，圆周角定理，相似三角形的性质和判定，三角形的外接圆与外心，三角形的内切圆与内心，等腰三角形的判定等知识点的理解和掌握，综合运用这些性质进行推理是解此题的关键．
练习册系列答案
相关题目
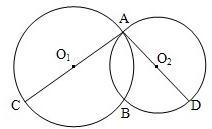25、如图，已知⊙O1和⊙O2相交于A、B，AC、AD分别是两圆的直径，
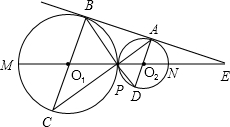长线交⊙O1于C点，BP的延长线交⊙O2于D点，直线O1O2交⊙O1于M，交⊙O2于N，与BA的延长线交于点E．
如图，⊙O和⊙O1分别是△ABC的外接圆和内切圆，两圆的半径分别为6和2，连接AO1并延长交⊙O于D，则AO1•O1D的值为