Question

如图，在矩形ABCD中，AB=6米，BC=8米，动点P以2米/秒的速度从点A出发，沿AC向点C移动，同时动点Q以1米/秒的速度从点C出发，沿CB向点B移动，当P、Q两点中其中一点到达终点时则停止运动．设P、Q两点移动t秒后，四边形ABQP的面积为S米．
（1）求面积S关于时间t的函数关系，并求出t的取值范围；
（2）在P、Q两点移动过程中，求当△PQC为等腰三角形时t的值．

Answer 1

解：（1）过点P作PE⊥BC于E，
在Rt△ABC中，米，
依题意有AP=2t，CQ=t，PC=10-2t．
由AB⊥BC，PE⊥BC，得PE∥AB，
∴，
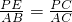即，
∴=，
即，
∵10-2t＞0，t＞0，
∴0＜t＜5，
答：面积S关于时间t的函数关系是S=t²-3t+24，t的取值范围是0＜t＜5．

（2）解：①当PC=QC时，有，
②当PQ=QC时，有（秒），
③当PQ=PC时，有（秒），
所以，当t为时，△PQC为等腰三角形，
答：当△PQC为等腰三角形时t的值为．
分析：（1）过点P作PE⊥BC于E，根据PE∥AB得到比例式，代入求出PE的长，根据S等于△ABC的面积减去△PQC的面积，代入求出即可；
（2）有三种情况：①PC=QC，②PQ=QC，③PQ=PC，代入得出关于t的方程，求出方程的解即可．
点评：本题主要考查对等腰三角形的性质，勾股定理，三角形的面积，矩形的性质，平行线分线段成比例定理等知识点的理解和掌握，能综合运用这些性质进行计算是解此题的关键．