题目内容
(2013•槐荫区二模)(1)分解因式:-4a2+4ab-b2;
(2)先化简,再求值:x(4-x)+(x+1)(x-1),其中x=
.
(2)先化简,再求值:x(4-x)+(x+1)(x-1),其中x=
| 1 | 2 |
分析:(1)原式提取-1变形后,利用完全平方公式分解即可;
(2)原式第一项利用单项式乘多项式法则计算,第二项利用平方差公式化简,去括号合并得到最简结果,将x的值代入计算即可求出值.
(2)原式第一项利用单项式乘多项式法则计算,第二项利用平方差公式化简,去括号合并得到最简结果,将x的值代入计算即可求出值.
解答:解:(1)原式=-(4a2-4ab+b2)
=-(2a-b)2;
(2)原式=4x-x2+x2-1
=4x-1,
当x=
时,原式=4×
-1=2-1=1.
=-(2a-b)2;
(2)原式=4x-x2+x2-1
=4x-1,
当x=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了整式的混合运算-化简求值,涉及的知识有:平方差公式,完全平方公式,单项式乘多项式法则,去括号法则,以及合并同类项法则,熟练掌握公式及法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•槐荫区二模)如图,直线y=-
(2013•槐荫区二模)如图,直线y=-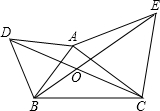 (2013•槐荫区二模)如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是
(2013•槐荫区二模)如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是 (2013•槐荫区二模)如图,在△ABC中AB=AC=10,CB=16,分别以AB,AC为直径作半圆,则图中阴影部分的面积是
(2013•槐荫区二模)如图,在△ABC中AB=AC=10,CB=16,分别以AB,AC为直径作半圆,则图中阴影部分的面积是