题目内容
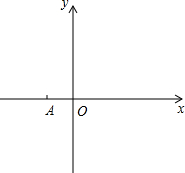 如图,在直角坐标平面上,点A、B在x轴上(A点在B点左侧),点C在y轴正半轴上,若A(-1,0),OB=3OA,且tan∠CAO=2.
如图,在直角坐标平面上,点A、B在x轴上(A点在B点左侧),点C在y轴正半轴上,若A(-1,0),OB=3OA,且tan∠CAO=2.
(1)求点B、C的坐标;
(2)求经过点A、B、C三点的抛物线解析式;
(3)P是(2)中所求抛物线的顶点,设Q是此抛物线上一点,若△ABQ与△ABP的面积相等,求Q点的坐标.
 解:(1)如图,∵点A、B在x轴上(A点在B点左侧),A(-1,0),OB=3OA,
解:(1)如图,∵点A、B在x轴上(A点在B点左侧),A(-1,0),OB=3OA,∴B(3,0).
又∵tan∠CAO=2,点C在y轴正半轴上,
∴
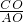 =2,则CO=2OA=2,
=2,则CO=2OA=2,∴C(0,2)
综上所述,点B、C的坐标分别是:(3,0),(0,2);
(2)∵该抛物线与x轴的两个交点坐标是:A(-1,0),B(3,0),
∴设过点A、B、C的抛物线解析式为y=a(x+1)(x-3)(a≠0).
把点C的坐标代入,得
2=a(0+1)(0-3),
解得,a=-
 ,
,则该抛物线的解析式为:y=-
 (x+1)(x-3)(或y=-
(x+1)(x-3)(或y=- x2+
x2+ x+2);
x+2);(3)由(2)中抛物线解析式得到:y=-
 (x-1)2+
(x-1)2+ ,则顶点P的坐标是(1,
,则顶点P的坐标是(1, ).
).∵△ABQ与△ABP的面积相等,且点Q是抛物线上的一点
∴点Q与点P到x轴的距离相等,
∴点Q是直线y=±
 与抛物线的交点.
与抛物线的交点.①当y=
 时,x=1,此时,点Q与点P重合,即Q(1,
时,x=1,此时,点Q与点P重合,即Q(1, );
);②当y=-
 时,-
时,- (x-1)2+
(x-1)2+ =-
=- ,
,解得,x1=1+2
 ,x2=1-2
,x2=1-2 ,此时,点Q的坐标是(1+2
,此时,点Q的坐标是(1+2 ,-
,- )或(1-2
)或(1-2 ,-
,- )
)综上所述,符合条件的点Q的坐标是:(1,
 )、(1+2
)、(1+2 ,-
,- )或(1-2
)或(1-2 ,-
,- ).
).分析:(1)根据已知条件“A(-1,0),OB=3OA,且tan∠CAO=2”易求点B、C的坐标;
(2)设抛物线解析式为y=a(x+1)(x-3)(a≠0).然后把点C的坐标分别代入,求得a的值;
(3)根据“同底等高的两个三角形的面积相等”可知,点Q是直线y=与抛物线的交点.
点评:本题考查了二次函数综合题.其中涉及到了坐标与图形的性质,锐角三角函数的定义,待定系数法求二次函数的解析式,以及一次函数与抛物线的交点问题.解答(2)题时,因为已知抛物线与x轴的两个交点坐标,所以设交点式关系式,可以减少繁琐的计算过程.

练习册系列答案
相关题目
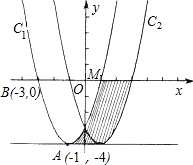 如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)
如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)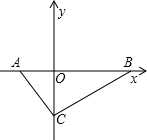 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC= 如图,在直角坐标平面内,函数y=
如图,在直角坐标平面内,函数y= 完成下列各题:
完成下列各题: 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是
如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是