Question

如图，已知A、B、C分别是⊙O上的点，∠B=60°，P是直径CD的延长线上的一点，且AP=AC.

（1）求证：AP与⊙O相切；

（2）如果AC=3，求PD的长.

Answer 1

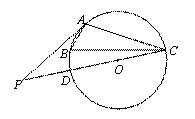
（1）证明：连接OA.

∵.

∴.

∴.

∵OA=OC,

∴.

∵AP=AC,

∴.

∴.

∴.

又∵点A在⊙O上，

∴PA是⊙O的切线.    

 (2)在Rt△PAO中，，

∴.

又∵AC=3，

∴AP=AC=3.

               根据勾股定理得: .   

∴，.

∴.