题目内容
已知∠AOB 内部有三条射线,其中,OE 平分∠BOC,OF 平分∠AOC.
(1)如图 1,若∠AOB=90°,∠AOC=30°,求∠EOF 的度数; 如图 2,若∠AOB=α,求∠EOF 的度数(用含 α 的式子表示);
(3)若将题中的“平分”的条件改为“∠EOB= 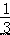 ∠COB,∠COF=
∠COB,∠COF= 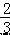 ∠COA”,且∠AOB=α,用含 α 的
∠COA”,且∠AOB=α,用含 α 的


【考点】角的计算;角平分线的定义.
【分析】(1)首先根据角平分线的定义求得∠COF,然后求得∠BOC 的度数,根据角平分线的定义 求得∠EOC,然后根据∠EOF=∠COF+∠EOC 求解;
根据角平分线的定义可以得到∠COF= 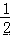 ∠AOC,∠EOC=
∠AOC,∠EOC= 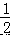 ∠BOC,然后根据
∠BOC,然后根据
∠EOF=∠COF+∠EOC=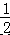 ∠AOC+
∠AOC+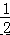 ∠BOC=
∠BOC=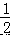 (∠AOC+∠BOC)即可得到;(3)根据
(∠AOC+∠BOC)即可得到;(3)根据
∠EOB= 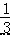 ∠COB,可以得到,∠EOC=
∠COB,可以得到,∠EOC= 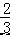 ∠COB,则
∠COB,则
∠EOF=∠EOC+∠COF= 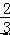 ∠BOC+
∠BOC+ 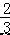 ∠AOC=
∠AOC=  ∠AOB,从而求解.
∠AOB,从而求解.
【解答】解:(1):(1)∵OF 平分∠AOC,
∴∠COF= 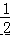 ∠AOC=
∠AOC= 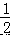 ×30°=15°,
×30°=15°,
∵∠BOC=∠AOB﹣∠AOC=90°﹣30°=60°,OE 平分∠BOC,
∴∠EOC= 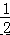 ∠BOC=30°,
∠BOC=30°,
∴∠EOF=∠COF+∠EOC=45°;
)∵OF 平分∠AOC,
∴∠COF= 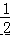 ∠AOC, 同理,∠EOC=
∠AOC, 同理,∠EOC= 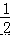 ∠BOC,
∠BOC,
∴∠EOF=∠COF+∠EOC= 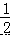 ∠AOC+
∠AOC+ 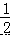 ∠BOC=
∠BOC= 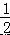 (∠AOC+∠BOC)=
(∠AOC+∠BOC)= 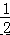 ∠AOB=
∠AOB=  α;
α;
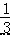 (3)∵∠EOB= ∠COB,
(3)∵∠EOB= ∠COB,

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案为了鼓励居民节约用水,万源市民生给排水公司对居民生活用水按阶梯式水价计费,下表是我 市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 12 吨以下(含 12 吨) | a | 0.15 |
| 超过 12 吨不超过 18 吨的部分 | b | |
| 超过 18 吨的部分 | 4.5 |
[说明:①每户产生的污水量等于该户的用水量;②水费=自来水费+污水处理费
(1)已知小李家 2013 年 4 月份用水量 16 吨,交水费 45.2 元;5 月份用水量 14 吨,交水费 37.9 元.求 表中 a、b 的值.
设小李家每月用水量为 x 吨,交水费 y 元,求 y(元)与 x(吨)的函数关系式,并指出自变量 x 的 取值范围.
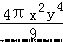 的系数与次数的积为
的系数与次数的积为 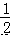 )+(x+
)+(x+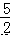 ),其中 x=﹣
),其中 x=﹣ .
.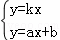 的解是 .
的解是 .