题目内容
如图，已知梯形ABCD中，AD∥BC，AB=AD=CD，BD⊥CD，则∠C等于
- A.30°
- B.45°
- C.60°
- D.75°
C
分析：根据AD∥BC，得∠ADB=∠CBD，再由AB=AD=CD，则∠ABD=∠ADB，由等腰梯形的性质，得∠ABC=∠C，设∠ABD=x，则∠C=2x，由BD⊥CD，得∠CBD+∠C=90°，即可解得x．
解答：∵AD∥BC，
∴∠ADB=∠CBD，
∵AB=AD，
∴∠ABD=∠ADB，
∵AB=CD，
∴∠ABC=∠C，
设∠ABD=x，∴∠C=2x，
∵BD⊥CD，∴∠BDC=90°，
∴∠CBD+∠C=90°，
∴x+2x=90°．
解得x=30°，
∴∠C=60°，
故选C．
点评：本题考查了等腰梯形的性质、等腰三角形的判定、三角形的内角和定理以及应用，要熟练掌握．
分析：根据AD∥BC，得∠ADB=∠CBD，再由AB=AD=CD，则∠ABD=∠ADB，由等腰梯形的性质，得∠ABC=∠C，设∠ABD=x，则∠C=2x，由BD⊥CD，得∠CBD+∠C=90°，即可解得x．
解答：∵AD∥BC，
∴∠ADB=∠CBD，
∵AB=AD，
∴∠ABD=∠ADB，
∵AB=CD，
∴∠ABC=∠C，
设∠ABD=x，∴∠C=2x，
∵BD⊥CD，∴∠BDC=90°，
∴∠CBD+∠C=90°，
∴x+2x=90°．
解得x=30°，
∴∠C=60°，
故选C．
点评：本题考查了等腰梯形的性质、等腰三角形的判定、三角形的内角和定理以及应用，要熟练掌握．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
9、如图，已知梯形ABCD中，AD∥BC，BE平分∠ABC，BE⊥CD，∠A=110°，AD=3，AB=5，则BC的长为（ ）
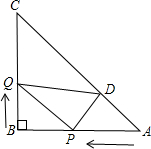点到达终点时，另一点也随之停止．过Q作QD∥AB交AC于点D，连接PD，设运动时间为t秒时，四边形BQDP的面积为s．
（2007•遂宁）如图，已知等腰△ABC的面积为4cm2，点D、E分别是AB、AC边的中点，则梯形DBCE的面积为