ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌдкЬнаЮABCDжаЃЌADЁЮBCЃЌЁЯABCЃН90ЁуЃЌcosCЃН![]() ЃЌDCЃН5ЃЌBCЃН6ЃЌвдЕуBЮЊдВаФЃЌBDЮЊАыОЖзїдВЛЁЃЌЗжБ№НЛБпCDЁЂBCгкЕуEЁЂFЃЎ
ЃЌDCЃН5ЃЌBCЃН6ЃЌвдЕуBЮЊдВаФЃЌBDЮЊАыОЖзїдВЛЁЃЌЗжБ№НЛБпCDЁЂBCгкЕуEЁЂFЃЎ
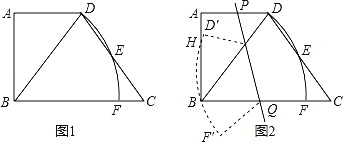
ЃЈ1ЃЉЧѓsinЁЯBDCЕФжЕЃЛ
ЃЈ2ЃЉСЊНсBEЃЌЩшЕуGЮЊЩфЯпDBЩЯвЛЖЏЕуЃЌШчЙћЁїADGЯрЫЦгкЁїBECЃЌЧѓDGЕФГЄЃЛ
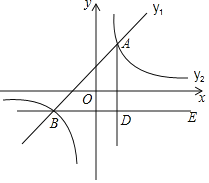
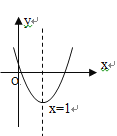
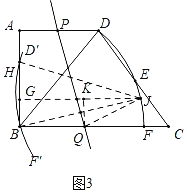
ЃЈ3ЃЉШчЭМ2ЃЌЕуPЁЂQЗжБ№ЮЊБпADЁЂBCЩЯЖЏЕуЃЌНЋЩШаЮDBFбизХжБЯпPQелЕўЃЌелЕўКѓЕФЛЁD'F'ОЙ§ЕуBгыABЩЯЕФвЛЕуHЃЈЕуDЁЂFЗжБ№ЖдгІЕуD'ЃЌF'ЃЉЃЌЩшBHЃНxЃЌBQЃНyЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЈВЛашвЊаДЖЈвхгђЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉyЃН
ЃЛЃЈ3ЃЉyЃН![]()
ЁОНтЮіЁП
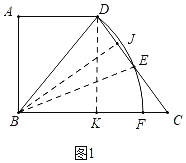
ЃЈ1ЃЉШчЭМ1жаЃЌСЌНгBEЃЌЙ§ЕуDзїDKЁЭBCгкKЃЌЙ§ЕуBзїBJЁЭCDгкJЃЎЯыАьЗЈЧѓГіBJЃЌBDМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉЗжСНжжЧщаЮЗжБ№ЧѓНтЃКЂйЕБЁїADGЁзЁїBCEЪБЃЎЂкЕБЁїADGЁзЁїECBЪБЃЌЗжБ№РћгУЯрЫЦШ§НЧаЮЕФаджЪЧѓНтМДПЩЃЎ
ЃЈ3ЃЉШчЭМ3жаЃЌЙ§ЕуBзїBJЁЭPQНЛ![]() гкJЃЌСЌНгBJЃЌJHЃЌJQЃЌЙ§ЕуJзїJGЁЭBHгкGЃЌЙ§ЕуQзїQKЁЭJHгкKЃЎгЩЬтвтBQЃНQJЃНyЃЌЧѓГіQKЃЌKJЃЌдкRtЁїQKJжаЃЌРћгУЙДЙЩЖЈРэМДПЩНтОіЮЪЬтЃЎ
гкJЃЌСЌНгBJЃЌJHЃЌJQЃЌЙ§ЕуJзїJGЁЭBHгкGЃЌЙ§ЕуQзїQKЁЭJHгкKЃЎгЩЬтвтBQЃНQJЃНyЃЌЧѓГіQKЃЌKJЃЌдкRtЁїQKJжаЃЌРћгУЙДЙЩЖЈРэМДПЩНтОіЮЪЬтЃЎ
ЃЈ1ЃЉШчЭМ1жаЃЌСЌНгBEЃЌЙ§ЕуDзїDKЁЭBCгкKЃЌЙ§ЕуBзїBJЁЭCDгкJЃЎ
дкRtЁїCDKжаЃЌЁпЁЯDKCЃН90ЁуЃЌCDЃН5ЃЌcosЁЯCЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрCKЃН3ЃЌ
ЁпBCЃН6ЃЌ
ЁрBKЃНCKЃН3ЃЌ
ЁпADЁЮBCЃЌЁЯABCЃН90ЁуЃЌ
ЁрЁЯAЃН90Ёу
ЁпDKЁЭBCЃЌ
ЁрЁЯAЃНЁЯABCЃНЁЯDKBЃН90ЁуЃЌ
ЁрЫФБпаЮABKDЪЧОиаЮЃЌ
ЁрADЃНBKЃН3ЃЌ
ЁрDBЃНDCЃН5ЃЌDKЃН![]() ЃН
ЃН![]() ЃН4ЃЌ
ЃН4ЃЌ
ЁпSЁїDCBЃН![]() BCDKЃН
BCDKЃН![]() CDBJЃЌ
CDBJЃЌ
ЁрBJЃН![]() ЃЌ
ЃЌ
ЁрDJЃН![]() ЃН
ЃН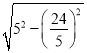 ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпBDЃНBEЃЌBJЁЭDEЃЌ
ЁрDJЃНJEЃН![]() ЃЌ
ЃЌ
ЁрECЃНCDЉDJЃНJEЃН5Љ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрsinЁЯBDCЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌ
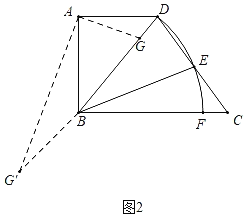
ЁпADЁЮBCЃЌ
ЁрЁЯADGЃНЁЯDBCЃЌ
ЁпDBЃНDCЃЌ
ЁрЁЯDBCЃНЁЯCЃЌ
ЁрЁЯADGЃНЁЯCЃЌ
ЁпЁїADGЯрЫЦЁїBECЃЌ
ЁргаСНжжЧщаЮЃКЕБЁїADGЁзЁїBCEЪБЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрDGЃН![]() ЃЌ
ЃЌ
ЕБЁїADGЁзЁїECBЪБЃЌ
![]() ЃН
ЃН![]() ЃЌ
ЃЌ
![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрDGЃН![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШчЭМ3жаЃЌЙ§ЕуBзїBJЁЭPQНЛ![]() гкJЃЌСЌНгBJЃЌJHЃЌJQЃЌЙ§ЕуJзїJGЁЭBHгкGЃЌЙ§ЕуQзїQKЁЭJHгкKЃЎ
гкJЃЌСЌНгBJЃЌJHЃЌJQЃЌЙ§ЕуJзїJGЁЭBHгкGЃЌЙ§ЕуQзїQKЁЭJHгкKЃЎ
гЩЬтвтЃКQBЃНQJЃНyЃЌBJЃНBDЃН5ЃЌ
ЁпJBЃНJHЃЌJGЁЭBHЃЌ
ЁрBGЃНGHЃН![]() xЃЌ
xЃЌ
ЁрJGЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпЁЯGBQЃНЁЯBGKЃНЁЯQKGЃН90ЁуЃЌ
ЁрЫФБпаЮBGKQЪЧОиаЮЃЌ
ЁрBQЃНGKЃНyЃЌQKЃНGBЃН![]() xЃЌ
xЃЌ
дкRtЁїQKJжаЃЌ
ЁпJQ2ЃНQK2+KJ2ЃЌ
Ёрy2ЃН![]() x2+ЃЈ
x2+ЃЈ![]() ЉyЃЉ2ЃЌ
ЉyЃЉ2ЃЌ
ЁрyЃН![]() ЃЎ
ЃЎ