题目内容
在平面上具有整数坐标的点称为整点.若一线段的端点分别为(2,11),(11,14),则在此线段上(包括端点)的整点共有
- A.3个
- B.4个
- C.6个
- D.8个
B
分析:根据题意,设经过点(2,11)、(11,14)的直线方程y=ax+b(a≠0),利用待定系数法求得该直线方程,然后在此线段上(包括端点)寻找整点.
解答: 解:设经过点(2,11)、(11,14)的直线方程y=ax+b(a≠0),则
解:设经过点(2,11)、(11,14)的直线方程y=ax+b(a≠0),则
 ,
,
解得, ,
,
∴所求的线段所在的直线方程为y= x+
x+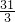 ;
;
①当y=12时,x=5,即整点(5,12)在该线段上;
②当y=13时,x=8,即整点(8,13)在该线段上;
又∵端点(2,11)、(11,14)也是整点,
∴在此线段上(包括端点)的整点共有4个;
故选B.
点评:本题考查了坐标与图形性质.解得该题的关键是求得此线段所在的直线的方程,根据该直线方程取y的整数值.
分析:根据题意,设经过点(2,11)、(11,14)的直线方程y=ax+b(a≠0),利用待定系数法求得该直线方程,然后在此线段上(包括端点)寻找整点.
解答:
 解:设经过点(2,11)、(11,14)的直线方程y=ax+b(a≠0),则
解:设经过点(2,11)、(11,14)的直线方程y=ax+b(a≠0),则 ,
,解得,
 ,
,∴所求的线段所在的直线方程为y=
 x+
x+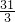 ;
;①当y=12时,x=5,即整点(5,12)在该线段上;
②当y=13时,x=8,即整点(8,13)在该线段上;
又∵端点(2,11)、(11,14)也是整点,
∴在此线段上(包括端点)的整点共有4个;
故选B.
点评:本题考查了坐标与图形性质.解得该题的关键是求得此线段所在的直线的方程,根据该直线方程取y的整数值.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目