Question

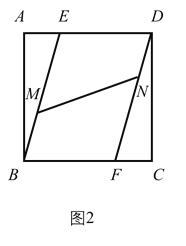
【题目】已知：如图，在中，分别在边的中点，是对角线，过点作，交的延长线于．

（1）求证：四边形是平行四边形；

（2）若四边形是矩形，则四边形是什么特殊四边形？并证明你的结论．

Answer 1

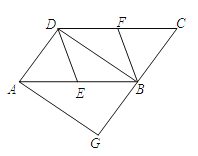
【答案】（1）见解析；（2）四边形是菱形，见解析

【解析】

（1）根据已知条件证明，，依据一组对边平行且相等的四边形是平行四边，从而得出四边形是平行四边形；

（2）四边形是矩形可证明，再根据邻边相等的平行四边形是菱形，从而得出结论．

（1）证明：∵四边形为平行四边形，

∴，

∵分别为边的中点，

∴，

∴，

∵，

∴四边形为平行四边形.

（2）解：四边形是菱形，理由如下：

∵四边形为平行四边形，

∴，

∵分别为边的中点，

∴，

∴，

∵，

∴四边形为平行四边形，

∴，

∵四边形是矩形，

∴，

∴，

∵，

∴四边形是平行四边形，

∴四边形是菱形.