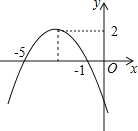Question

【题目】如图，已知在平面直角坐标系xOy中，抛物线y=ax2+2x+c与x轴交于点A（﹣1，0）和点B，与y轴相交于点C（0，3），抛物线的对称轴为直线．

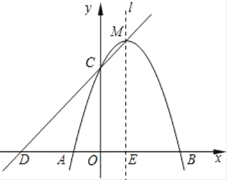
（1）求这条抛物线的关系式，并写出其对称轴和顶点M的坐标；

（2）如果直线y=kx+b经过C、M两点，且与x轴交于点D，点C关于直线的对称点为N，试证明四边形CDAN是平行四边形；

Answer 1

【答案】（1）y=-x2+2x+3；（2）详见解析.

【解析】

（1）将A、C两点坐标代入解析式即可求出a、c，将解析式配成顶点式即可得到对称轴方程和顶点坐标；

（2）先由C、M两点坐标求出直线CM解析式，进而求出D点坐标，由于C、N两点关于抛物线对称轴对称，则CN‖AD，同时可求出N点坐标，然后得出CN=AD，即可得出结论.

（1）∵抛物线y=ax2+2x+c经过点A（-1，0）和点C（0，3），

∴，

∴，

∴

故对称轴为直线x=1，顶点M（1，4）；

（2）如图：

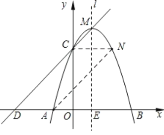
∵点C关于直线的对称点为N，

∴N（2，3），

∵直线y=kx+b经过C、M两点，

∴，

∴，

∴y=x+3，

∵y=x+3与x轴交于点D，

∴D（-3，0），

∴AD=2=CN

又∵AD‖CN，

∴CDAN是平行四边形.