Question

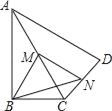
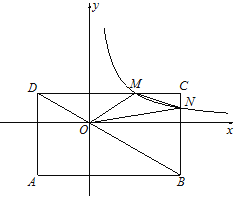
【题目】如图，矩形ABCD的对角线BD经过坐标原点O，矩形的边分别平行于坐标轴，反比例函数(k＞0)的图象分别与BC、CD交于点M、N．若点A(－2，－2)，且△OMN的面积为，则k＝( )

(A)2.5 (B)2 (C)1.5 (D)1

Answer 1

【答案】B

【解析】分析：过点M作MQ⊥x轴于点Q，由S四边形EOF＝S四边形CHOG，设C(a，)，分别用含a，k的式子表示点M，N的坐标，根据S△OMN＝S梯形MNGQ.列方程求k.

详解：过点M作MQ⊥x轴于点Q，

因为S四边形EOF＝S四边形CHOG，所以CG·CH＝4，

设C(a，)，则M(，)，N(a，).

S△OMH＝S△ONG＝S△OMQ＝，

因为S五边形OMNG＝S△OMN＋S△ONG＝S△OMQ＋S梯形MNGQ.

所以S△OMN＝S梯形MNGQ.

则)(a－)，解得k＝2.

故选B.